
|
Match Editorial |
Friday, March 17, 2006
Match summary
With the TCO stimulating our coding adrenalin to the max, a high number of registrants in regular SRMs has ceased to surprise us. With 898 competitors, this match was no exception. Because of a small technical problem, the coding phase started 10 minutes later. This was no impediment for the code enthusiasts and the match was prolonged with 10 minutes, as expected. The problems were not very tricky this time and, because of the clarifying examples, the number of challenges was relatively low.
In Division 1, Petr added another victory to his impressive record. kalinov took the second place and mathijs came in third.
In division 2, only three coders managed to solve all the problems. Daumilas, the winner, is also the proud owner of a score of 1111.1. Newcomer Daumilas claimed the second spot, and Michael.tamm finished the third.
The Problems
Aquarium

Used as: Division Two - Level One:
Value 250 Submission Rate 374 / 478 (78.24%) Success Rate 314 / 374 (83.96%) High Score otoc for 247.81 points (2 mins 40 secs) Average Score 184.24 (for 314 correct submissions)
The most straightforward way to solve this problem is so simply check every possible size of Bob in the range [minSize, maxSize]. You can then compare each of these possible sizes with the size of every fish in the aquarium. If any conflict is detected, the size of Bob that arose the conflict is discarded. Below is the source code in Java that solves this problem:
public int peaceful(int minSize, int maxSize, int[] fishSizes) {
int n = fishSizes.length;
int sol = 0;
for (int i = minSize; i <=maxSize ; i++) {
boolean ok = true;
for (int j = 0; j < n; j++) {
if (i >= 2 * fishSizes[j] && i <= 10 * fishSizes[j]) ok = false;
if (fishSizes[j] >= 2 * i && fishSizes[j] <= 10 * i) ok = false;
}
if (ok) sol++;
}
return sol;
}
Another simple method that was used a lot is to build a boolean array of size 1000, where the i-th element represents whether Bob can have a size of i or not. Then, for every fish in the aquarium, you mark with "false" all the elements in the array that represent wrong sizes for Bob. In the end you count how many elements of the array with indices between minSize and maxSize are "true".
ScrabbleBet


Used as: Division Two - Level Two:
Used as: Division One - Level One:
Value 500 Submission Rate 124 / 478 (25.94%) Success Rate 94 / 124 (75.81%) High Score JBoy for 448.69 points (9 mins 50 secs) Average Score 279.01 (for 94 correct submissions)
Value 300 Submission Rate 282 / 350 (80.57%) Success Rate 268 / 282 (95.04%) High Score NauCoder for 297.51 points (2 mins 36 secs) Average Score 219.65 (for 268 correct submissions)
Although ScrabbleBet was a pretty classical problem of probability theory, there are quite a few different approaches one could use to get around.
For the math fans, this problem can be solved in a few lines with the formula of binomial distribution. Let us denote the number of games played in a meeting by n, the number of wins you need by r and the probability of winning one game by p. Then, the chances you have to win one meeting are given by the following formula:
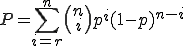
However, this problem can be solved without knowing the complicate formula above. Knowing the following two more basic formulas is also good enough:

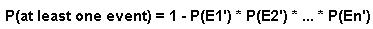
For the second part, you just apply the second formula with each event having the probability we computed earlier.
For more details, refer to the Understanding Probabilities tutorial.
A math free, and also easy to code solution, is to use a dynamic programming approach. Denote with c[n][r] the chance of winning at least r games out of n with a chance of p to win one single game. Then, you can compute c as follows:
c[n][r] = 1, if r = 0
c[n][r] = 0, if n = 0 and r > 0
c[n][r] = p* c[n-1][r-1] + (1-p)*c[n-1][r], otherwise.
In the end, you should return 1 - c[games][winsNeeded] ^ trials
For more information on the use of DP in probability problems, check the Step by Step Probability Computation chapter. Bingo


By dgoodman
Used as: Division Two - Level Three:
Used as: Division One - Level Two:
Value 1000 Submission Rate 16 / 478 (3.35%) Success Rate 6 / 16 (37.50%) High Score Burunduk2 for 499.82 points (37 mins 31 secs) Average Score 389.12 (for 6 correct submissions)
Value 450 Submission Rate 209 / 350 (59.71%) Success Rate 105 / 209 (50.24%) High Score ploh for 386.33 points (11 mins 56 secs) Average Score 247.18 (for 105 correct submissions)
Because there are quite a lot of rules to follow (and of course the examples didn't cover them all), this problem had the lowest success rate in both divisions.
The last sentence of the problem statement, "If the call that first allows you to win allows you to win in more than one way, the method must return the winning sequence that had the earliest call in it" must be carefully analyzed and properly understood in order to proceed with the algorithm. The first thing to note is that once you have a winning sequence, the method winner should return something. That is, from this moment the game is over (you won) and the remaining calls should be ignored. Because the last call can simultaneously produce more than one winning sequence, you are told to select the one that had the earliest call in it. Then ... you have to read the whole problem statement again. You want to know what happens if there are more winning sequences with the same first call. Unfortunately you don't find this information anywhere in the statement. But working on a paper with concrete examples (this is usually a wise thing to do), you quickly realize that such a situation is not possible. From coder to coder, this analysis can take varying amounts of time. As the clock starts from the moment you open the problem, this time is of course significant. To find out more on how to deal with problems like this, you may want to read the How To Dissect a TopCoder Problem Statement tutorial.
Then, coding is quite straightforward. Represent the grid as a matrix with 5 lines and 5 columns, and mark on it the calls in the order they appear. After each new call, you should check every line, column and main diagonal to see if a winning sequence has been reached. The code in Java is given below:
public class Bingo{
int[][] idx = new int[5][5];
int[] win = new int[5];
public String winner(String[] card, String[] call){
int[][] a = new int[5][5];
for (int r = 0; r < 5; r++){
String[] x = card[r + 1].trim().split("[ ]+");
for (int c = 0; c < 5; c++) {
if (c !=2 || r != 2)
a[r][c] = Integer.parseInt(x[c]);
}
}
for (int r = 0; r < 5; r++) for (int c = 0; c < 5; c++) idx[r][c] = -1;
idx[2][2] = 99;
for (int i = 0; i < call.length-1;i++) {
int v = Integer.parseInt(call[i].substring(1));
for (int r = 0; r < 5; r++)for (int c = 0; c < 5; c++)
if (a[r][c] == v) idx[r][c] = i;
}
win[4] = 100; // winning index
for (int r = 0; r < 5; r++) getWin(r,0,0,1);
for (int c = 0; c < 5; c++) getWin(0,c,1,0);
getWin(0, 0, 1, 1); getWin(0, 4, 1, -1);
if (win[4] == 100) return "YOU LOSE";
String ret="";
for (int i = 0;i < 5; i++) if (i == 0 || win[i] != win[i - 1])
ret += "," + call[win[i]];
return ret.substring(1);
}
void getWin(int r, int c, int dr, int dc){
int[] w = new int[5];
for (int i = 0; i < 5; i++) w[i] = idx[r + i * dr][c + i * dc];
Arrays.sort(w);
if (w[4] == 99) w[4] = w[3];
if (w[0] == -1 || w[4] > win[4]) return;
if (w[4] == win[4] && w[0] > win[0]) return;
win = w;
}
CirclesOfDestruction


Used as: Division One - Level Three:
Value 1000 Submission Rate 21 / 350 (6.00%) Success Rate 14 / 21 (66.67%) High Score Petr for 783.21 points (15 mins 53 secs) Average Score 581.25 (for 14 correct submissions)
This problem is actually not as hard as it seems. Suppose you want to reach from a point A to a point X on the edge of the map. What's the quickest way to get there? If there are no obstacles, it is of course a straight line. The only reason you may want to deviate from the straight line is an expanding circle that reaches to an intermediary point on the segment AX before you. This means that the distance between a point of the circle and X is smaller than the distance between you and X. But because the speed of the circle is the same as yours, you will never be able to catch up. So, it's an all or nothing game - you can either reach a destination point by moving on a straight line, or you can not reach it at all.
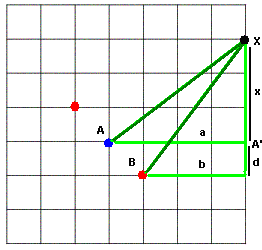
You may need to treat separately the case when B is on the AA' segment. In that case every point on the axis is obstructed, so there are no solutions there.
