March 23, 2020 Single Round Match 770 Editorials
MaximumMoves
Used as: Division Two – Level One:
| Value | 250 |
| Submission Rate | 195 / 237 (82.28%) |
| Success Rate | 94 / 195 (48.21%) |
| High Score | kshitij_sodani for 246.76 points (3 mins 15 secs) |
| Average Score | 202.98 (for 94 correct submissions) |
Every number greater than 1 can be written using the sum of several twos and threes, for example, 7 = 2 + 2 + 3. The number n, needs n / 2 (rounded down) summands. For example, 7 needs 3 summands. 20 needs 10 summands.
If p > q or q – p = 1, the answer is -1. Else, the answer is (q – p) / 2 (rounded down).
def getMaximumMoves(self, p, q):
if p>q:
return -1
if p==q:
print(0)
d=q-p
if d==1:
return -1
if d%2==0:
return d//2
else:
return d//2
LayeredGlass
Used as: Division Two – Level Two:
| Value | 500 |
| Submission Rate | 116 / 237 (48.95%) |
| Success Rate | 87 / 116 (75.00%) |
| High Score | yongwhan for 436.60 points (11 mins 9 secs) |
| Average Score | 287.84 (for 87 correct submissions) |
Each glass has 2 options to flip or not to flip and 4 options to rotate. We check each of the options for each glass and find the minimum. Note that we can skip 4 options of rotation of one of the glasses.
Here is the code (by cntswj):
def rotate(self, a):
n = len(a)
ret = [[None] * n for _ in range(n)]
for i in range(n):
for j in range(n):
ret[j][n - i - 1] = a[i][j]
ret = [''.join(row) for row in ret]
return ret
def flip(self, a):
n = len(a)
ret = [[None] * n for _ in range(n)]
for i in range(n):
for j in range(n):
ret[i][j] = a[i][n - j - 1]
ret = [''.join(row) for row in ret]
return ret
def check(self, a, b):
n = len(a)
ret = 0
for i in range(n):
for j in range(n):
if a[i][j] == 'X' or b[i][j] == 'X':
ret += 1
return ret
def minDefects(self, a, b):
n = len(a)
ret = n * n
for _ in range(2):
for _ in range(4):
ret = min(ret, self.check(a, b))
b = self.rotate(b)
b = self.flip(b)
return ret
DeleteArrays
Used as: Division Two – Level Three:
| Value | 900 |
| Submission Rate | 15 / 237 (6.33%) |
| Success Rate | 5 / 15 (33.33%) |
| High Score | taran_1407 for 481.22 points (33 mins 24 secs) |
| Average Score | 431.97 (for 5 correct submissions) |
Used as: Division One – Level One:
| Value | 300 |
| Submission Rate | 110 / 167 (65.87%) |
| Success Rate | 89 / 110 (80.91%) |
| High Score | Petr for 245.04 points (14 mins 7 secs) |
| Average Score | 168.45 (for 89 correct submissions) |
Let’s solve the problem case by case:
- One of the arrays is longer than the sum of the length of the other arrays.
Consider this array be A, sort A, some of the first elements of A will remain and others will be deleted using the first and third type of move. - The total number of elements is odd.
An element will remain, the smallest element of an array. - The general case.
Note that the number of moves we should do on a particular type of move is fixed. For example, consider a = b = c = 4. We must use the first, second, and, third type of move 2 times each.
In fact, we should solve a system of equations with three variables.
The following code uses the NumPy library to solve the system of equations (by wilkluka).
def doDelete(self, a, b, c, x, y, z):
A = [33, 42]
for i in xrange(2, a):
A.append((5 * A[i - 1] + 7 * A[i - 2]) % 1000000007 + 1)
B = [13]
for i in xrange(1, b):
B.append((11 * B[i - 1]) % 1000000007 + 1)
C = [7, 2]
for i in xrange(2, c):
C.append((5 * C[i - 1] + 7 * C[i - 2]) % 1000000007 + 1)
mm = 0
aa = len(A)
bb = len(B)
cc = len(C)
if aa > bb+cc:
A.sort()
n = aa-bb-cc
mm = sum(A[:n])
A = A[n:]
elif bb > aa + cc:
B.sort()
n = bb - aa - cc
mm = sum(B[:n])
B = B[n:]
elif cc > aa + bb:
C.sort()
n = cc - aa - bb
mm = sum(C[:n])
C = C[n:]
if (len(A) + len(B) + len(C)) % 2 == 1:
mm = min(A)
cost = x + z
tb = A
if (mm == min(B) and cost < x + y) or (mm > min(B)):
mm = min(B)
cost = x + y
tb = B
if (mm == min(C) and cost < y + z) or (mm > min(C)):
mm = min(C)
cost = z + y
tb = C
tb.remove(mm)
a = np.array([[1, 1, 0], [0, 1, 1], [1, 0, 1]])
b = np.array([len(A), len(B), len(C)])
solutions = np.linalg.solve(a, b).astype(int)
return mm, (solutions * np.array([z, x, y])).sum() + sum(A) + sum(B) + sum(C)
And a c++ code (by ecnerwal):
vector<long long> doDelete(int NA, int NB, int NC, long long wx, long long wy, long long wz) {
vector<ll> A(NA);
vector<ll> B(NB);
vector<ll> C(NC);
A[0] = 33;
A[1] = 42;
for (int i = 2; i <= NA-1; i++) {
A[i] = (5*A[i-1] + 7*A[i-2]) % 1000000007 + 1;
}
B[0] = 13;
for (int i = 1; i <= NB-1; i++) {
B[i] = (11*B[i-1]) % 1000000007 + 1;
}
C[0] = 7;
C[1] = 2;
for (int i = 2; i <= NC-1; i++) {
C[i] = (5*C[i-1] + 7*C[i-2]) % 1000000007 + 1;
}
sort(A.begin(), A.end());
sort(B.begin(), B.end());
sort(C.begin(), C.end());
vector<ll> V[3];
V[0] = A;
V[1] = B;
V[2] = C;
int N[3];
N[0] = NA;
N[1] = NB;
N[2] = NC;
ll W[3][3];
memset(W, 0, sizeof(W));
W[0][1] = W[1][0] = wx;
W[1][2] = W[2][1] = wy;
W[0][2] = W[2][0] = wz;
ll S = 0;
for (int z = 0; z < 3; z++) {
for (int i = 0; i < N[z]; i++) {
S += V[z][i];
}
}
for (int z = 0; z < 3; z++) {
int x = (z+1)%3, y = (z+2) % 3;
if (N[z] >= N[x] + N[y]) {
ll ans = 0;
for (int i = 0; i < N[z] - N[x] - N[y]; i++) {
ans += V[z][i];
}
return {ans, N[x] * W[z][x] + N[y] * W[z][y] + (S - ans)};
}
}
int s = (N[0] + N[1] + N[2]) / 2;
if ((N[0] + N[1] + N[2]) & 1) {
vector<ll> ans;
for (int z = 0; z < 3; z++) {
int x = (z+1)%3, y = (z+2) % 3;
vector<ll> cnd({V[z][0], W[x][y] * (s - (N[z]-1)) + W[y][z] * (s - N[x]) + W[x][z] * (s - N[y]) + (S - V[z][0])});
if (z == 0) {
ans = cnd;
} else {
ans = min(ans, cnd);
}
}
return ans;
} else {
return {0, W[0][1] * (s - N[2]) + W[1][2] * (s - N[0]) + W[2][0] * (s - N[1]) + S};
}
}
ShoppingSpree
Used as: Division One – Level Two:
| Value | 450 |
| Submission Rate | 79 / 167 (47.31%) |
| Success Rate | 42 / 79 (53.16%) |
| High Score | Stonefeang for 424.48 points (7 mins 3 secs) |
| Average Score | 315.28 (for 42 correct submissions) |
The problem is similar to find maximum-weight matching in bipartite graphs (solve it before continuing). One of the methods for solving the problem is to use minimum cost flow (read the article before you continue).
For each vertex like v, the first time we choose an edge which connects v to another vertex, we gain value of it, but next times we gain nothing.
So, here is the edges we should add:
- Source to every shirt. Cost = -shirtValue[i]. Capacity = 1.
- Source to every shirt. Cost = 0. Capacity = infinity.
- Every jean to sink. Cost = -jeanValue[i]. Capacity = 1.
- Every jean to sink. Cost = 0. Capacity = infinity.
- shirtType[i] to jeansType[i]. Cost = 0. Capacity = infinity.
Now when we calculate the minimum cost, it’s the answer. Three notes:
- We can use k instead of infinity.
- We should limit the initial flow from source to k.
- We want to use the maximum gain but the algorithm calculates the minimum cost flow, so we need to set negative costs.
// flow part
struct kra {
int cel, *prze1, *prze2;
ll koszt;
};
int n=0, zr, uj;
const ll inf=1e9;
vector <vector <kra>> graf;
vector <int> bylo, aktu;
vector <ll> odl, pamodl;
void vert(int v) {
if (v>n) {
n=v;
graf.resize(n);
bylo.resize(n);
aktu.resize(n);
odl.resize(n);
pamodl.resize(n);
}
}
void add_edge(int v, int u, int prze, ll koszt) {
vert(v+1); vert(u+1);
kra ret1{u, new int(prze), new int(0), koszt};
kra ret2{v, ret1.prze2, ret1.prze1, -koszt};
graf[v].push_back(ret1);
graf[u].push_back(ret2);
}
void spfa() {
for (int i=0; i<n; i++) {
aktu[i]=1;
pamodl[i]=inf;
}
aktu[zr]=pamodl[zr]=0;
queue <int> kol;
kol.push(zr);
while(!kol.empty()) {
int v=kol.front();
kol.pop();
if (aktu[v])
continue;
aktu[v]=1;
for (kra i : graf[v]) {
if (*i.prze1 && pamodl[v]+i.koszt<pamodl[i.cel]) {
pamodl[i.cel]=pamodl[v]+i.koszt;
aktu[i.cel]=0;
kol.push(i.cel);
}
}
}
}
void dij() {
for (int i=0; i<n; i++)
odl[i]=inf;
priority_queue < pair <ll,int> > dijks;
dijks.push({0, zr});
while(!dijks.empty()) {
ll dis=-dijks.top().first;
int v=dijks.top().second;
dijks.pop();
if (odl[v]!=inf)
continue;
odl[v]=pamodl[v]+dis;
for (auto j : graf[v])
if ((*j.prze1) && odl[j.cel]==inf)
dijks.push({-(dis+pamodl[v]-pamodl[j.cel]+j.koszt), j.cel});
}
}
int dfs(int v) {
if (v==uj)
return 1;
bylo[v]=1;
for (int i=0; i<(int)graf[v].size(); i++) {
if (!bylo[graf[v][i].cel] && (*graf[v][i].prze1) &&
odl[v]+graf[v][i].koszt==odl[graf[v][i].cel] && dfs(graf[v][i].cel)) {
(*graf[v][i].prze1)--;
(*graf[v][i].prze2)++;
return 1;
}
}
return 0;
}
pair <int,ll> flow(int zrzr, int ujuj, int moge) {
zr=zrzr; uj=ujuj;
vert(zr+1); vert(uj+1);
spfa();
pair <int,ll> ret{0, 0};
for (int i=0; i<moge; i++) {
//~ dij();
spfa();
odl=pamodl;
for (int i=0; i<n; i++)
bylo[i]=0;
if (!dfs(zr))
break;
ret.first++;
ret.second+=odl[uj];
}
return ret;
}
};
// end of flow part
struct ShoppingSpree
{
int maxValue(int k, vector <int> shirtValue, vector <int> jeansValue, vector <int> shirtType, vector <int> jeansType)
{
MinCost pawel;
int n=shirtValue.size();
int m=jeansValue.size();
int d=shirtType.size();
for (int i=0; i<n; i++)
{
pawel.add_edge(0, i+1, 1, -shirtValue[i]);
pawel.add_edge(0, i+1, k, 0);
}
for (int i=0; i<m; i++)
{
pawel.add_edge(n+1+i, n+m+1, 1, -jeansValue[i]);
pawel.add_edge(n+1+i, n+m+1, k, 0);
}
for (int i=0; i<d; i++)
{
pawel.add_edge(1+shirtType[i], n+1+jeansType[i], k, 0);
}
return -pawel.flow(0, n+m+1, k).second;
}
};
Used as: Division One – Level Three:
| Value | 900 |
| Submission Rate | 20 / 167 (11.98%) |
| Success Rate | 12 / 20 (60.00%) |
| High Score | bqi343 for 758.95 points (12 mins 44 secs) |
| Average Score | 560.09 (for 12 correct submissions) |
We add zero to the array and sort it at the first. Refer to this link next. The problem can be solved in the same way. Let’s calculate P(MAX < x), the probability that maximum (MAX) be less than x.
Note that P(MAX < x) is a piecewise function. For a[i] < x < a[i + 1],
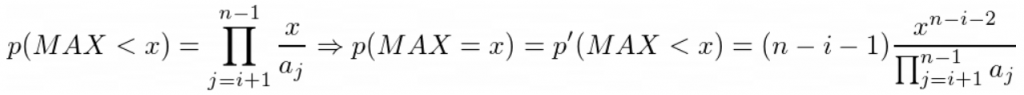
Note that array is zero-based and the function above just works in range (a[i], a[i + 1]).
Let’s calculate the mathematical expectation (in the range (a[i], a[i + 1])):
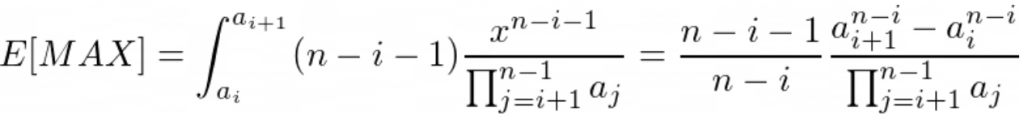
auto A = Aprefix;
ll state = seed;
while (sz(A) < n) {
state = (1103515245 * state + 12345) % (1LL<<31);
A.pb(T+(state%Amod));
}
A.pb(0);
sort(all(A));
ld ans = A.back();
ld prod = 1;
ROF(i,1,sz(A)) {
int k = sz(A)-i;
ld p1 = A[i]*prod; // two zeroes?
ld p2 = 0;
if (A[i] != 0) {
prod *= pow((ld)A[i-1]/A[i],k);
p2 = A[i-1]*prod;
}
ans -= (p1-p2)/(k+1);
}
return ans;
misof


