September 20, 2017 Single Round Match 719 Editorials
Some of the SRM 719 Editorials are now published. Check out the editorials of the interesting SRM 719 problems below. Thanks to Shizhouxing,nitish_and square1001 for contributing to the editorials. If you wish to discuss the problems or editorials you may do it in the discussion forum here.
SRM 719 Round 1 – Division II, Level One – LongLiveZhangzj by Shizhouxing
 We need to count the number of words that are exciting in speech.
We need to count the number of words that are exciting in speech.
For each word s[i] in speech, we just check whether there is a word in words which is exactly the same as s[i]. If so, word s[i] is considered to be exciting.
The answer to the problem is the number of exciting words in speech.
Code:
#include <bits/stdc++.h>
using namespace std;
class LongLiveZhangzj
{
public:
int donate(vector <string> speech, vector <string> words)
{
int ans = 0;
for (auto x:speech) {
int exciting = 0;
for (auto y:words)
if (x == y) exciting = 1;
ans += exciting;
}
return ans;
}
};
SRM 719 Round 1 – Division II, Level Two – LongMansionDiv2 – by nitish_
In total, it will be optimal to move only (N + M – 1) steps where N – the number of rows, M – the number of columns.This problem is a problem of a shortest path in a 2-D grid. Weights for crossing each box are given in an int[].The best solution for this problem is by greedy approach.
Reason for this is that it is optimal to choose a row with minimum weight and move horizontally across that row only because it will add minimum weight to the solution. Thus, the solution will be equal:
ans = M*(minumum_weight_among_all_rows) + cost_of_single_step_on_every_other_row.
Code:
#include <bits/stdc++.h>
using namespace std;
class LongMansionDiv2 {
public:
long long minimalTime(int M, vector <int> t) {
long long ans = 0;
long long sum = 0;
for(int i =0; i < t.size(); ++i)
sum += t[i];
long long minm = *min_element(t.begin(), t.end());
ans = minm*M + sum - minm;
return ans;
}
};
Note: use long long to avoid overflow.
Complexity: O(N), since we iterate over the input array.
SRM 719 Round 1 – Division II, Level Three – TwoDogsOnATree by nitish_
Firstly, root the tree at vertex 0. In a tree, between any two nodes, there is exactly only one path. Hence, in order to solve this problem, we should be able to find the XOR of all the weights on the path as quickly as possible. This can be done in O(N) preprocessing and O(1) for query.
Find the XOR of edges of all the vertex from the root vertex and store it in XOR[].
Thus, XOR[x] will store the XOR of all the edges in the path between node x and the root. Now to compute this between any two vertex (x , y), simply xor the XOR[x]^XOR[y] in O(1). This statement is true, because if vertex x and y lie different side of root, then the path must go through the root, and one path is kind of extension of another. Otherwise, if they lie on the same side of root, then the repeated edges are disabled with xor operation, because x^x = 0; and 0^x = x. That’s why the above statement is correct.
Now, suppose you choose a pair of nodes (a,b) for DOG 1 and another pair of nodes (c,d) for DOG 2. If there is no common edge between the two paths, then the result of A XOR B i.e. A^B = (XOR[a] ^ XOR[B])^(XOR[C]^XOR[d]), where A and B were results for first and second paths respectively.
Now, consider the other case, when there is overlapping of edges, then in that case, we can choose another permutation formed with same set of nodes which does not overlap i.e : either {(a, c) ,(b,d)} or {(a,d), (b,c)}. Result for any of these combination would result same as above. A^B = (XOR[a] ^ XOR[B])^(XOR[C]^XOR[d]).
Thus, the problem reduces to choosing 4 vertex a, b, c, d for which the XOR[a]^XOR[b]^XOR[C]^XOR[d] is maximum.
To solve this, There are many methods:
Firstly, make a set of distinct values of all the pairs from the available nodes. This will give you maximum of N*N distinct values.
Now, among all these pairs, Take the XOR of all pairs and return the maximum from it.
Code:
#include <vector>
#include <set>
#include <algorithm>
#include <cmath>
using namespace std;
class TwoDogsOnATree {
public:
int XOR[1020];
int maximalXorSum(vector<int> parent, vector<int> w)
{
int n = parent.size() + 1;
int ans = 0;
set<int> st;
for (int i = 1; i < n; ++i) {
XOR[i] = XOR[parent[i - 1]] ^ w[i - 1];
}
for (int i = 0; i < n; ++i) {
for (int j = 0; j < i; ++j)
st.insert(XOR[i] ^ XOR[j]);
}
set<int>::iterator it1;
set<int>::iterator it2;
for (it1 = st.begin(); it1 != st.end(); ++it1) {
for (it2 = st.begin(); it2 != st.end(); ++it2)
ans = max(ans, *it1 ^ *it2);
}
return ans;
}
};
Complexity: O(N ^ 4), since there will be N^2 elements in st set.
SRM 719 Round 1 – Division I, Level One – LongMansionDiv1 by square1001

Make problem more simple
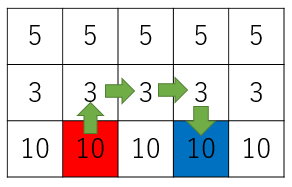

You are given a grid with H (H ≤ 50) rows by W (W ≤ 109) columns. Cell in i-th row and j-th column denotes (i, j). Each cell in a grid has written a positive integer. Also, each cell in the same row has written the same value ai. You are given the position of starting cell (sx, sy) and finishing cell (gx, gy). You can move to 4-directions (up, down, right, left). Calculate the minimum sum of numbers written in passed cells.
The solution
The optimal solution is, amazingly, can always construct by following 3 steps. Pay attention that is assuming sy ≤ gy (because if sy > gy you can swap start and goal).
a. Move some cells upwards or downwards.
b. Move right gy-sy times.
c. Move some cells upwards or downwards and reach goal.
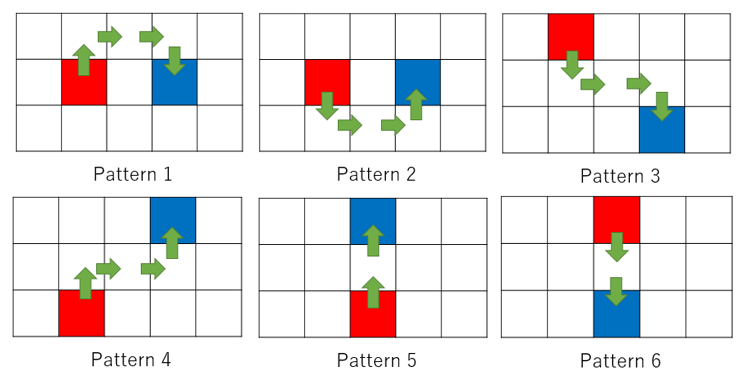
You can choose row which uses in step b (row of finishing step a). In the constraint H ≤ 50, you can brute-force and get minimum of it. Also, you can calculate the cost of the path in O(H), so the total time complexity is O(H2).
Why this is optimal?
1. Moving extra left and right direction is not good
Moving left and right more times than shortest, is a waste of cost. Why? You can see from the picture.
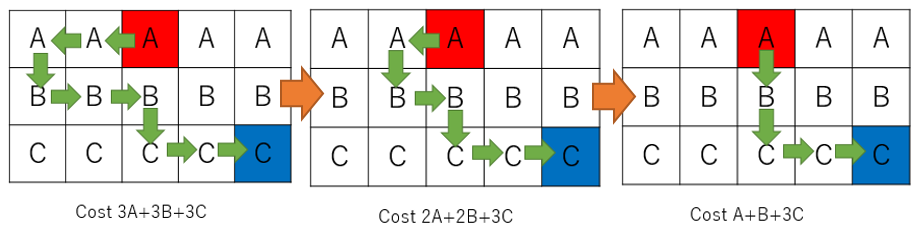
You can erase the left arrow (assuming sy ≤ gy) and corresponding right arrow. Also, you can move the disconnected part one cell right. As all numbers in same row is same, the reduced cost is always the cost in left arrow row and plus cost in right arrow row, so it is always higher than zero.
2. Moving right in different row is not good
First, see the example in the picture.
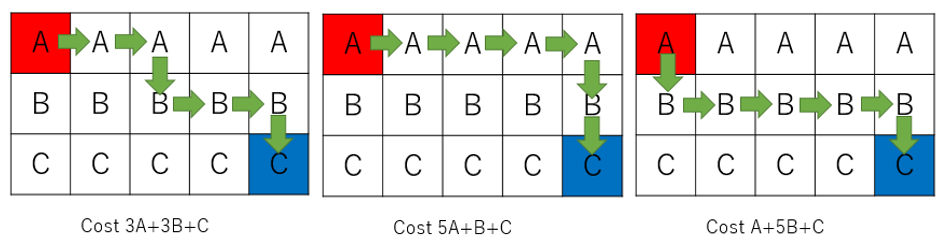
In this example, the left one costs 3A+3B+C, the middle one costs 5A+B+C, and the right one costs A+5B+C. You can see that for any real number A, B, C, 3A+3B+C≤max(5A+B+C,A+5B+C). You can prove it by solving in case of A>B, A=B, A<B, and using that the number in the same row is the same. And, in any pattern, you can reduce zero or more cost with “two row that uses right arrow to one row”, like left to middle or right one in the example.
If you do operation in 1. and 2. completely, you can get the path that can get from 3 steps that I first mentioned. So it means the optimal solution is in one of the way which can get from “3 steps”.
Code:
#include <cmath>
#include <vector>
#include <algorithm>
using namespace std;
class LongMansionDiv1 {
public:
long long minimalTime(vector<int> v, int sx, int sy, int ex, int ey) {
int n = v.size();
long long ret = 1LL << 62;
for (int i = 0; i < n; i++) {
long long res = 1LL * v[i] * (abs(sy - ey) - 1);
for (int j = min(sx, i); j <= max(sx, i); j++) res += v[j];
for (int j = min(ex, i); j <= max(ex, i); j++) res += v[j];
ret = min(ret, res);
}
return ret;
}
};
Bonus: Also, if you use prefix sum technique, you can get the answer in time complexity O(H). Let’s think about the solution!
Harshit Mehta
Sr. Community Evangelist


