By boba5551– Topcoder Member
Discuss this article in the forums
Introduction
Notation
Basic idea
Isolating the last bit
Read cumulative frequency
Change frequency at some position and update tree
Read the actual frequency at a position
Scaling the entire tree by a constant factor
Find index with given cumulative frequency
2D BIT
Lazy modification
Sample problem
Conclusion
References
Introduction
We often need some sort of data structure to make our algorithms faster. In this article we will discuss about the Binary Indexed Trees structure, proposed by Peter M. Fenwick. This structure was first used for data compression, Peter M. Fenwick. In algorithmic contests it is often used for storing frequencies and manipulating cumulative frequency tables. We begin by motivating the use of this structure by an example.
Consider the following problem: There are n boxes that undergo the following queries:
add marble to box i
sum marbles from box k to box l
Our goal is to implement those two queries.
The naive solution has time complexity of O(1) for query 1 and O(n) for query 2. Suppose we make m queries. The worst case (when all the queries are 2) has time complexity O(n * m). Using some data structure (i.e. RMQ) we can solve this problem with the worst case time complexity of O(m log n). Another approach is to use the Binary Indexed Tree data structure, also with the worst time complexity O(m log n) — but Binary Indexed Trees are easier to code and require less memory space than RMQ.
Notation
Before we proceed with defining the structure and stating the algorithms, we introduce some notations:
BIT - Binary Indexed Tree
MaxIdx - maximum index which will have non-zero frequency
f[i] - frequency at index i, i = 1 … MaxIdx
c[i] - cumulative frequency at index i (f[1] + f[2] + … + f[i])
tree[i] - the sum of frequencies stored at index i of BIT (latter we will describe which frequencies correspond to i); we will be using “tree frequency” to refer to “sum of frequencies stored at an index of BIT”
num¯ - complement of integer num (integer where each binary digit is inverted: 0 -> 1; 1 -> 0 )
NOTE: We set f[0] = 0, c[0] = 0, tree[0] = 0, so sometimes we will ignore index 0.
Basic idea
Each integer can be represented as a sum of powers of two. In the same way, a cumulative frequency can be represented as a sum of sets of subfrequencies. In our case, each set contains some successive number of non-overlapping frequencies.
Let idx be an index of BIT. Let r be the position in idx of its last non-zero digit in binary notation, i.e., r is the position of the least significant non-zero bit of idx. tree[idx] holds the sum of frequencies for indices (idx - 2^r + 1) through idx, inclusive (see Table 1.1 for clarification). We also write that idx is responsible for indices from (idx - 2^r + 1) to idx (“responsibility” is the main notion that we will use in describing our algorithms).
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| f | 1 | 0 | 2 | 1 | 1 | 3 | 0 | 4 | 2 | 5 | 2 | 2 | 3 | 1 | 0 | 2 |
| c | 1 | 1 | 3 | 4 | 5 | 8 | 8 | 12 | 14 | 19 | 21 | 23 | 26 | 27 | 27 | 29 |
| tree | 1 | 1 | 2 | 4 | 1 | 4 | 0 | 12 | 2 | 7 | 2 | 11 | 3 | 4 | 0 | 29 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| tree | 1 | 1…2 | 3 | 1…4 | 5 | 5…6 | 7 | 1…8 | 9 | 9…10 | 11 | 9…12 | 13 | 13…14 | 15 | 1…16 |
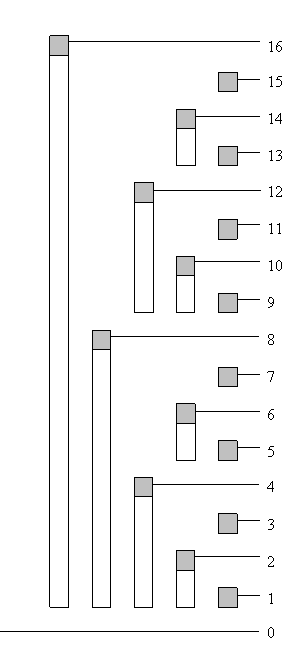
Image 1.3 – tree of responsibility for indices (bar shows range of
frequencies accumulated in top element)

Image 1.4 – tree with tree frequencies
Suppose that we want to find the cumulative frequency at index 13, i.e., the sum of the first 13 frequencies. In binary notation, 13 is equal to 1101. Interestingly, in this example it holds c[1101] = tree[1101] + tree[1100] + tree[1000] (we will reveal this connection in more detail later).
Isolating the last bit
NOTE: For the sake of brevity, we will use “the last bit” to refer to the least significant non-zero bit of the corresponding integer.
The algorithms for BIT require extracting the last bit of a number, so we need an efficient way of doing that. Let num be an integer. We will now show how to isolate the last bit of num. In binary notation num can be represented as a1b, where a represents binary digits before the last bit and b represents zeroes after the last bit.
Integer -num is equal to (a1b)¯ + 1 = a¯0b¯ + 1. b consists of all zeroes, so b¯ consists of all ones. Finally we have
-num = (a1b)¯ + 1 = a¯0b¯ + 1 = a¯0(0…0)¯ + 1 = ¯0(1…1) + 1 = a¯1(0…0) = a¯1b.
Now, we can easily isolate the last bit of num, using the bitwise operator AND (in C++, Java it is &) between num and -num:
1
2
3
4
a1b
&
a¯ 1 b——————– = (0… 0) 1(0… 0)
In what follows, we describe some methods used for manipulating BITs, e.g., read a cumulative frequency, update a frequency, find, etc.
Reading cumulative frequency
To compute the cumulative frequency at index idx, we perform the following sequence of steps: add tree[idx] to sum (initially, we set sum to be zero); subtract the last bit of idx from itself (i.e., set the least significat non-zero bit of idx to zero); and repeat this process while idx is greater than zero. The following function (written in C++) implements this approach:
1
2
3
4
5
6
7
8
int read(int idx) {
int sum = 0;
while (idx > 0) {
sum += tree[idx];
idx -= (idx & -idx);
}
return sum;
}
We provide an example for idx = 13; sum = 0:
| iteration | idx | position of the last bit | idx & -idx | sum |
|---|---|---|---|---|
| 1 | 13 = 1101 | 0 | 1 (2 ^0) | 3 |
| 2 | 12 = 1100 | 2 | 4 (2 ^2) | 14 |
| 3 | 8 = 1000 | 3 | 8 (2 ^3) | 26 |
| 4 | 0 = 0 | — | — | — |
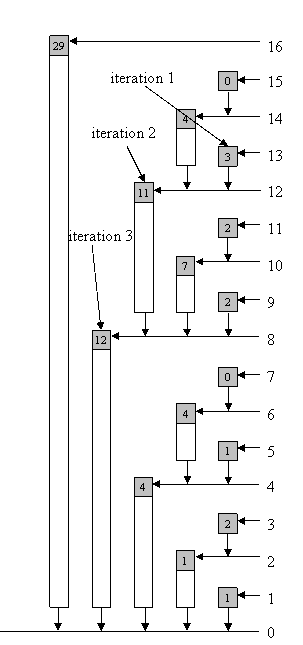
Image 1.5 – the arrows show the path from an index to zero which is used to compute sum (the image shows example for index 13)
So, our result is 26. The number of iterations in this function is the number of non-zero bits in idx, which is at most log MaxIdx.
Time complexity: O(log MaxIdx).
Code length: Up to ten lines.
Change frequency at some position and update tree
We now illustrate how to perform a BIT update. That is, we show how to update BIT at all the indices which are responsible for the frequency that we are changing. Assume that we want to increase the frequency at index idx by val. As a reminder, to read the cumulative frequency at some index we repeatedly remove the last bit of the corresponding index and accumulate the corresponding tree frequency. To update the BIT corresponding to the increase of the frequency at idx by val, we apply the following steps: increment the tree frequency at the current index by val (the starting index is the one whose frequency has changed); add the last bit of idx to itself; and, repeat while idx is less than or equal to MaxIdx. The corresponding function in C++ follows:
1
2
3
4
5
6
void update(int idx, int val) {
while (idx <= MaxIdx) {
tree[idx] += val;
idx += (idx & -idx);
}
}
Note that the functions read and update in some sense perform inverse operations of each other – in read we subtract while in update we add the last bit of the current index.
The following example illustrates update for idx = 5:
| iteration | idx | position of the last bit | idx & -idx |
|---|---|---|---|
| 1 | 5 = 101 | 0 | 1 (2 ^0) |
| 2 | 6 = 110 | 1 | 2 (2 ^1) |
| 3 | 8 = 1000 | 3 | 8 (2 ^3) |
| 4 | 16 = 10000 | 4 | 16 (2 ^4) |
| 5 | 32 = 100000 | — | — |
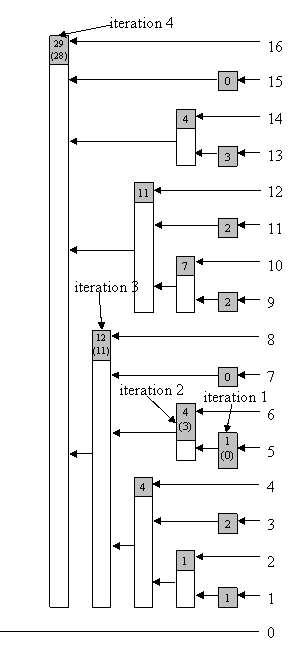
Image 1.6 – Updating a tree (in the brackets are tree frequencies before the update); the arrows show the path while the tree is being updated from index to MaxIdx (the image shows an example for index 5)
Using the algorithm above or following the arrows shown in Image 1.6 we can update BIT.
Time complexity: O(log MaxIdx).
Code length: Up to ten lines.
Read the actual frequency at a position
We have described how to read the cumulative frequency at a given index. Assume that we want to get the actual frequency at index idx. It is obvious that we can not simply return tree[idx] to achieve that. One approach to get the frequency at a given index is to maintain an additional array. In this array, we separately store the frequency for each index. Reading or updating a frequency takes O(1) time; the memory space is linear. However, it is also possible to obtain the actual frequency at a given index without using additional structures.
First, the frequency at index idx can be calculated by calling the function read twice – f[idx] = read(idx) – read(idx – 1) — by taking the difference of two adjacent cumulative frequencies. This procedure works in 2 * O(log n) time. There is a different approach that has lower running time complexity than invoking read twice, lower by a constant factor. We now describe this approach.
The main idea behind this approach is motivated by the following observation. Assume that we want to compute the sum of frequencies between two indices. For each of the two indices, consider the path from the index to the root. These two paths meet at some index (at latest at index 0), after which point they overlap. Then, we can calculate the sum of the frequencies along each of those two paths until they meet and subtract those two sums. In that way we obtain the sum of the frequencies between that two indices.
We translate this observation to an algorithm as follows. Let x be an index and y=x-1. We can represent (in binary notation) y as a0b, where b consists of all ones. Then, x is a1b¯ (note that b¯ consists of all zeros). Now, consider the first iteration of the algorithm read applied to x. In the first iteration, the algorithm removes the last bit of x, hence replacing x by z=a0b¯.
Now, let us consider how the active index idx of the function read changes from iteration to iteration on the input y. The function read removes, one by one, the last bits of idx. After several steps, the active index idx becomes a0b¯ (as a reminder, originally idx was equal to y=a0b), that is the same as z. At that point we stop as the two paths, one originating from x and the other one originating from y, have met. Now, we can write our algorithm that resembles this discussion. (Note that we have to take special care in case x equals 0.) A function in C++:
1
2
3
4
5
6
7
8
9
10
11
12
13
int readSingle(int idx) {
int sum = tree[idx]; // this sum will be decreased
if (idx > 0) { // the special case
int z = idx - (idx & -idx);
idx--; // idx is not important anymore, so instead y, you can use idx
while (idx != z) { // at some iteration idx (y) will become z
sum -= tree[idx];
// substruct tree frequency which is between y and "the same path"
idx -= (idx & -idx);
}
}
return sum;
}
Here is an example for getting the actual frequency for index 12:
First, we calculate z = 12 – (12 & -12) = 8, sum = 11
| iteration | y | position of the last bit | y & -y | sum |
|---|---|---|---|---|
| 1 | 11 = 1011 | 0 | 1 (2 ^0) | 9 |
| 2 | 10 = 1010 | 1 | 2 (2 ^1) | 2 |
| 3 | 8 = 1000 | — | — | — |
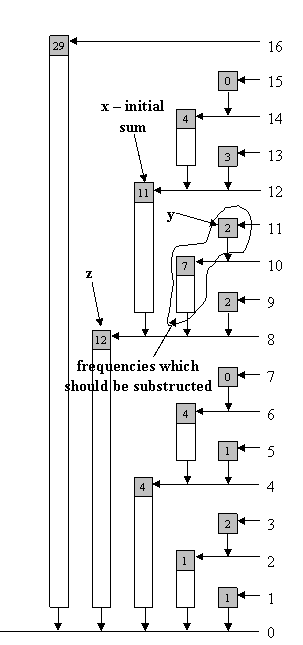
Image 1.7 – read the actual frequency at some index by using BIT (the image shows an example for index 12)
It is clear from the algorithm that it runs faster than invoking read twice – the while loop corresponds to a single invocation of read. Furthermore, for any odd number this algorithm runs in constant time.
Time complexity: O(log MaxIdx).
Code length: Up to fifteen lines.
Scaling the entire tree by a constant factor
Now we describe how to scale all the frequencies by a factor c. Simply, each index idx is updated by -(c – 1) * readSingle(idx) / c (because f[idx] – (c – 1) * f[idx] / c = f[idx] / c). The corresponding function in C++ is:
1
2
3
4
void scale(int c) {
for (int i = 1; i <= MaxIdx; i++)
update(-(c - 1) * readSingle(i) / c, i);
}
This can also be done more efficiently. Namely, each tree frequency is a linear composition of some frequencies. If we scale each frequency by some factor, we also scale a tree frequency by that same factor. Hence, instead of using the procedure above, which has time complexity O(MaxIdx * log MaxIdx), we can achieve time complexity of O(MaxIdx) by the following:
1
2
3
4
void scale(int c) {
for (int i = 1; i <= MaxIdx; i++)
tree[i] = tree[i] / c;
}
Time complexity: O(MaxIdx).
Code length: Just a few lines.
Find index with given cumulative frequency
Consider a task of finding an index which corresponds to a given cumulative frequency, i.e., the task of perfoming an inverse operation of read. A naive and simple way to solve this task is to iterate through all the indices, calculate their cumulative frequencies, and output an index (if any) whose cumulative frequency equals the given value. In case of negative frequencies it is the only known solution. However, if we are dealing only with non-negative frequencies (that means cumulative frequencies for greater indices are not smaller) we can use an algorithm that runs in a logarithmic time, that is a modification of binary search. The algorithms works as follows. Iterate through all the bits (starting from the highest one), define the corresponding index, compare the cumulative frequency of the current index and given value and, according to the outcome, take the lower or higher half of the interval (just like in binary search). The corresponding function in C++ follows:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
// If in the tree exists more than one index with the same
// cumulative frequency, this procedure will return
// some of them
// bitMask - initialy, it is the greatest bit of MaxIdx
// bitMask stores the current interval that should be searched
int find(int cumFre) {
int idx = 0; // this variable will be the output
while (bitMask != 0) {
int tIdx = idx + bitMask; // the midpoint of the current interval
bitMask >>= 1; // halve the current interval
if (tIdx > MaxIdx) // avoid overflow
continue;
if (cumFre == tree[tIdx]) // if it is equal, simply return tIdx
return tIdx;
else if (cumFre > tree[tIdx]) {
// if the tree frequency "can fit" into cumFre,
// then include it
idx = tIdx; // update index
cumFre -= tree[tIdx]; // update the frequency for the next iteration
}
}
if (cumFre != 0) // maybe the given cumulative frequency doesn't exist
return -1;
else
return idx;
}
// If in the tree exists more than one index with a same
// cumulative frequency, this procedure will return
// the greatest one
int findG(int cumFre) {
int idx = 0;
while (bitMask != 0) {
int tIdx = idx + bitMask;
bitMask >>= 1;
if (tIdx > MaxIdx)
continue;
if (cumFre >= tree[tIdx]) {
// if the current cumulative frequency is equal to cumFre,
// we are still looking for a higher index (if exists)
idx = tIdx;
cumFre -= tree[tIdx];
}
}
if (cumFre != 0)
return -1;
else
return idx;
}
Example for cumulative frequency 21 and function find:
First iteration - tIdx is 16; tree[16] is greater than 21; halve bitMask and continue
Second iteration - tIdx is 8; tree[8] is less than 21, so we should include first 8 indices in result, remember idx because we surely know it is part of the result; subtract tree[8] of cumFre (we do not want to look for the same cumulative frequency again – we are looking for another cumulative frequency in the rest/another part of tree); halve bitMask and continue
Third iteration - tIdx is 12; tree[12] is greater than 9 (note that the tree frequencies corresponding to tIdx being 12 do not overlap with the frequencies 1-8 that we have already taken into account); halve bitMask and continue
Fourth iteration - tIdx is 10; tree[10] is less than 9, so we should update values; halve bitMask and continue
Fifth iteration - tIdx is 11; tree[11] is equal to 2; return index (tIdx)
Time complexity: O(log MaxIdx).
Code length: Up to twenty lines.
2D BIT
BIT can be used as a multi-dimensional data structure. Suppose you have a plane with dots (with non-negative coordinates). There are three queries at your disposal:
set a dot at (x , y)
remove the dot from (x , y)
count the number of dots in rectangle (0 , 0), (x , y) – where (0 , 0) is down-left corner, (x , y) is up-right corner and sides are parallel to x-axis and y-axis.
If m is the number of queries, max_x is the maximum x coordinate, and max_y is the maximum y coordinate, then this problem can be solved in O(m * log (max_x) * log (max_y)) time as follows. Each element of the tree will contain an array of dimension max_y, that is yet another BIT. Hence, the overall structure is instantiated as tree[max_x][max_y]. Updating indices of x-coordinate is the same as before. For example, suppose we are setting/removing dot (a , b). We will call update(a , b , 1)/update(a , b , -1), where update is:
1
2
3
4
5
6
7
void update(int x, int y, int val) {
while (x <= max_x) {
updatey(x, y, val);
// this function should update the array tree[x]
x += (x & -x);
}
}
The function updatey is the “same” as function update provided in the beginning of this note:
1
2
3
4
5
6
void updatey(int x, int y, int val) {
while (y <= max_y) {
tree[x][y] += val;
y += (y & -y);
}
}
These two functions can also be written as two nested loop:
1
2
3
4
5
6
7
8
9
10
11
void update(int x, int y, int val) {
int y1;
while (x <= max_x) {
y1 = y;
while (y1 <= max_y) {
tree[x][y1] += val;
y1 += (y1 & -y1);
}
x += (x & -x);
}
}
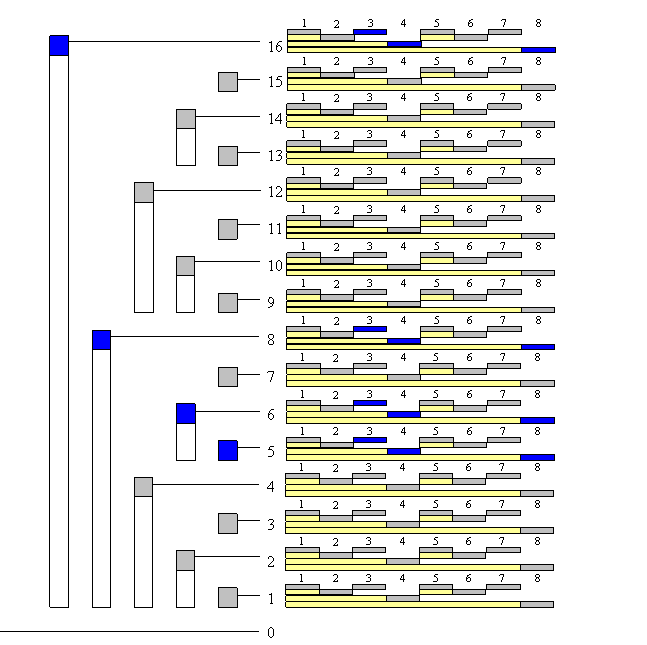
Image 1.8 – BIT is array of arrays, so this is two-dimensional BIT (size 16 x 8). Blue fields are fields which we should update when we are updating index (5 , 3).
The modification for other functions is very similar. Also, note that BIT can be used as an n-dimensional data structure.
Lazy Modification
So far we have presented BIT as a structure which is entirely allocated in memory during the initialization. An advantage of this approach is that accessing tree[idx] requires a constant time. On the other hand, we might need to access only tree[idx] for a couple of different values of idx, e.g. log n different values, while we allocate much larger memory. This is especially aparent in the cases when we work with multidimensional BIT.
To alleviate this issue, we can allocate the cells of a BIT in a lazy manner, i.e. allocate when they are needed. For instance, in the case of 2D, instead of defining BIT tree as a two-dimensional array, in C++ we could define it as map<pair<int, int>, int>. Then, accessing the cell at position (x, y) is done by invoking tree[make_pair(x, y)]. This means that those (x, y) pairs that are never needed will never be created. Since every query visits O(log (max_x) * log (max_y)) cells, if we invoke q queries the number of allocated cells will be O(q log (max_x) * log (max_y)).
However, now accessing (x, y) requires logarithmic time in the size of the corresponding map structure representing the tree, compared to only constant time previously. So, by losing a logarithmic factor in the running time we can obtain memory-wise very efficient data structure that per query uses only O(log (max_x) * log (max_y)) memory in 2D case, or only O(log MaxIdx) memory in the 1D case.
Sample problem
Problem 2:
Statement:
There is an array consisting of n cards. Initially, each card is put on the table with its face down. There are two queries:
T i j (switch the side of each card from index i to index j, inclusive –- each card with face down becomes with face up; each card with face up becomes with face down)
Q i (output 0 if the i-th card is face down, otherwise output 1)
Solution:
This problem has a solution based on BIT that for each query has time complexity O(log n).
First, we instantiate an array f of length n + 1. (The array f is not a BIT.) On a query “T i j” we set f[i]++ and f[j + 1]–-. In this way, for each card k between i and j, inclusive, the sum f[1] + f[2] + … + f[k] is increased by 1, and for all the other cards that sum remains the same as before (see Image 2.0 for clarification). To answer a query “Q k”, we compute the described cumulative sum (that can be seen as a cumulative frequency) and output it modulo 2.
 Image 2.0
Image 2.0Use BIT to increase/decrease the entries of f and to efficiently read the corresponding cumulative frequency.
Conclusion
Binary Indexed Trees are very easy to code.
Each query on Binary Indexed Tree takes constant or logarithmic time.
Binary Indexeds Tree require linear memory space.
You can use it as an n-dimensional data structure.
The space requirement can be additionaly optimized by lazily allocating BIT cells, while in the same time losing only logarithmic factor in the running time.
References
[1] RMQ
[2] Binary Search
[3] Peter M. Fenwick