July 7, 2018 TCO18 Algorithm Round 3A Editorials

This is the first of two round 3s and the competition is getting tougher. Only 600 people have made it to this round, but only 100 will move on (50 in round 3A and 50 in round 3B). Participants also have a chance to win a t-shirt if they score a positive number of points in either of the rounds.
Round 3A’s easy and medium problem are authored by [misof], while the hard one is authored by [ltdtl]. The editorials are all by [lg5293].

LeftToRightGame

In this problem, Alice and Bob are playing a game where they take alternating turns writing the digits of a positive integer from left to right. The game ends once there are exactly N digits, and Bob wins if and only if the number is divisible by D. Your task is given N and D, determine the winner of the game if both players play optimally.
There are a few ways to solve this problem and I’ll go over two of them. One is by dynamic programming and the other by casework. The dynamic programming approach is a bit “brainless” and doesn’t require any careful thinking, but may take longer to code. The casework approach is much faster to code but is much easier to get wrong if you miss a case.

Dynamic Programming Approach (dp)

To do dp, our state space is how many digits are left, what the current modulus is for the divisor, and the result is whether the current player will win. To get the winner of a particular state, we can check all subsequent states they can reach. The state is winnable if they can reach a state that is a losing state.
Here is a sample implementation (in java)

    int L, D;
    int[][] memo;
    int getWinner(int digitsWritten, int remainder) {
        if (digitsWritten == L) {
            if (remainder == 0) return 2; else return 1;
        }
        if (memo[digitsWritten][remainder] != 0) {
            return memo[digitsWritten][remainder];
        }
        if (digitsWritten == 0) {
            for (int d=1; d<=9; ++d) if (getWinner(1,d%D)==1) return memo[digitsWritten][remainder] = 1;
            return memo[digitsWritten][remainder] = 2;
        }
        if (digitsWritten % 2 == 0) {
            for (int d=0; d<=9; ++d) if (getWinner(digitsWritten+1,(remainder*10+d)%D)==1) return memo[digitsWritten][remainder] = 1;
            return memo[digitsWritten][remainder] = 2;
        }
        for (int d=0; d<=9; ++d) if (getWinner(digitsWritten+1,(remainder*10+d)%D)==2) return memo[digitsWritten][remainder] = 2;
        return memo[digitsWritten][remainder] = 1;
    }
    String whoWinsDP(int length, int divisor) {
        L = length;
        D = divisor;
        memo = new int[length][divisor];
        for (int l=0; l<L; ++l) for (int d=0; d<D; ++d) memo[l][d] = 0;
        int answer = getWinner(0,0);
        return answer == 1 ? "Alice" : "Bob";
    }

The advantage of this approach is that it is very easy to prove correctness and it is relatively easy to code. The disadvantage is that it does take a bit more time to type.
The runtime of this approach is the number of states times the number of subsequent states we can reach, which in this case is O(N * D).

Casework approach

Next, this is the approach by casework: it’s easy to see that if D = 1, then Bob always wins no matter what either player does, so let’s assume D > 1 now.
Now, we claim that the player that goes last almost decides the entire game. For instance, if Alice goes last, she has 10 choices of the last digit, and one of them is guaranteed to not cause the number to be divisible by D, so she can always win if she goes last (short justification, not all choices can be divisible by D when D > 1). So, for now, let’s assume N is even (i.e. Bob goes last).
For Bob, it is not always the case that he has a valid winning choice, for example, consider the case when N = 2, and D = 12. If Alice chooses the first digit to be 5, there is no valid choice for the second digit for Bob that makes the number divisible by 12.
If D <= 10, Bob can win since he has a choice of 10 digits, and since the gap between divisors is less than 10, he always has a valid winning choice. For D = 11, Bob can choose to always copy Alice’s move, so he has a winning strategy. Now, let’s say D >= 12. We want to claim on Alice’s last turn (i.e. the second to last turn in the game), she can choose a digit that gives Bob no winning choices. Let’s say for each choice 0,1,2,…,9 for Alice that Bob has a corresponding winning choice. Since D >= 10, Bob has at most one winning choice for each of Alice’s choice. Let the winning choices be a_0, a_1, …, a_9. We must have a_i = a_(i-1) + (D – 10). However this will make some a_i bigger than 10, which is a contradiction, which shows Alice has a winning strategy.
So, recapping, the logic is, if D = 1, then Bob wins, otherwise if N is odd, Alice wins, otherwise, if D <= 11, then Bob wins.
This can be checked in the following python code:

class LeftToRightGame:
	def whoWins(self, length, divisor):
		return (divisor == 1 or (length % 2 == 0 and divisor <= 11)) * "Bob" or "Alice"

This only checks a constant number of conditions, so this code takes O(1) time.

ProductThreshold

In this problem, you would like to know how many subarrays in an array have a product that doesn’t exceed a particular threshold. This array can be pretty large, so a sub-quadratic solution is required.
This is almost a standard problem. For instance, if you know all elements are positive, you can do a 2-pointer approach to solve this. However, here, there can be negative and zero elements in the array, so 2-pointers doesn’t work out of the box, and we need to be more careful in how we approach this problem. For example, consider an array like [2, -2, 2, -2, 2, -2, …], with a threshold of 1. The valid endpoints for a particular start point don’t form a contiguous range, which makes 2 pointers not work.
Instead of counting subarrays that stay below a threshold, let’s instead count subarrays that exceed the threshold and subtract it from the total number of subarrays. The reason for doing it is that it is easier to constrain these types of subarrays a bit more, in particular, none of these subarrays can contain zeros.
To exceed a particular threshold, we can naively iterate through the first log_2(10^9) non-one elements. So for each start point, we can naively scan from left to right on non-one elements until we exceed our product. We also want to make sure our product is positive after this point, so we can also keep track of how many elements have a positive or negative product.
To implement this, I scanned from right to left, and for each start point, I computed how many ending indices have a positive / negative suffix product. If I hit a zero, I reset all counts to zero (since no subarrays that exceed the limit can contain a zero). I also keep track of a stack of all non-one elements, which I can use to iterate through until I exceed the limit. After finding the point at which I always exceed the limit, I can use the previously computed counts of product / negative suffix products to compute how many elements after have the same parity (thus will be a positive product).

class ProductThreshold:
	def subarrayCount(self, n, limit, aprefix, spread, offset):
		p = len(aprefix)
		a = [0 for __ in xrange(n)]
		for i in range(p):
			a[i] = aprefix[i]
		seed = abs(a[p-1])
		for i in range(p,n):
			seed = (seed * 1103515245 + 12345) & ((1 << 31) - 1)
			a[i] = (seed % spread) + offset
		total = n * (n + 1) / 2
		nr = [[0, 0] for __ in xrange(n+1)]
		idx = 0
		nr[n][0] = 1
		stack = []
		for i in range(n-1, -1, -1):
			if a[i] == 0:
				idx = 0
				stack = []
			else:
				if a[i] < 0: idx = 1 - idx if abs(a[i]) > 1:
					stack.append((abs(a[i]), i))
				nr[i][0] = nr[i+1][0]
				nr[i][1] = nr[i+1][1]
				nr[i][idx] += 1
				w = 1
				si = len(stack)-1
				while si >= 0 and w * stack[si][0] <= limit: w *= stack[si][0] si -= 1 if si >= 0:
					total -= nr[stack[si][1]+1][idx]
		return total

The runtime of this code is O(n * log_2(10^9)).

ColoringEdgesDiv1

In this problem, we are given a 3-regular graph, and we would like to colour the edges of the graph with two colours such that no cycle is all the same colour. If there are multiple solutions, we can return any of them. Here, I’ll describe two different approaches

Solution 1

We show a solution always exists by constructing one. Here is a linear-time solution (O(V+E)) that takes advantage of 3-regularity of the given graph.
There are three main phases to this algorithm. All steps in each phase are done “simultaneously” (for the proof later).
[1] First, colour the edges such that no vertex has all 3 of its incident edges as the same colour.
This can be done via a max-flow algorithm, or by adding a dummy node connected to all vertices and finding a Eulerian tour which would guarantee that each vertex has at least one incident edge of each colour. This can be done in linear time.
[2] Once this is done, identify all monochromatic cycles in linear time (all these cycles will be vertex disjoint, due to 3-regularity, and the fact that each node has at most 2 adjacent edges of the same colour). For each cycle, pick one edge arbitrarily and flip its colour. Do this simultaneously for all cycles at once.
[3] Then, check if new monochromatic cycles are introduced (old cycles are guaranteed to be gone by now — this is easy to prove due to 3-regularity). For each new monochromatic cycle C, it is clear that at least one edge e on C was re-coloured in the previous step. Choose one of these edges arbitrarily and recall which cycle it belonged to before the colour-flip — let’s call it C’. On C’, choose one of the two adjacent edges to e and flip its colour as well as flip the colour of e (the colour of e will go back to its original colour). Do this for all new cycles simultaneously. This can all be done in linear time. This guarantees that there is no monochromatic cycle left (we’ll prove this now).
To observe why this solution works, let’s consider what happens at the end of step [1]. All monochromatic cycles are vertex-disjoint (due to 3-regularity). In addition, all new cycles introduced after step [2] are also vertex-disjoint (again, due to 3-regularity) Moreover, every vertex has at most two incident edges of the same color after step [1], [2], and [3], respectively (note we do all flips “simultaneously”). We’ll skip a formal proof, but this fact (referred to as (*)) is used in the proof later.
Let us now show that there is no monochromatic cycle after step [3].
Consider the edges that are coloured as 0 after step [3]. We’ll show that there is no cycle of colour 0 after step [3] (by symmetry the same holds for colour 1).
In step [3], we want to show that no 0-colour cycle is created by colouring some edge from 1 to 0.
Consider some 0-colour cycle C at the beginning of step [3] (after step [2]). Suppose we pick some edge e = (x, y) on cycle C and color it (back) to 1 and pick its neighboring edge e’ = (y, z) on the cycle C’ (that is a 1-colored cycle at the beginning of step [2]) and color it to 0. Clearly, neither C nor C’ is monochromatic after step [3].
This is a picture of C and C’ at the beginning of step [3]

 
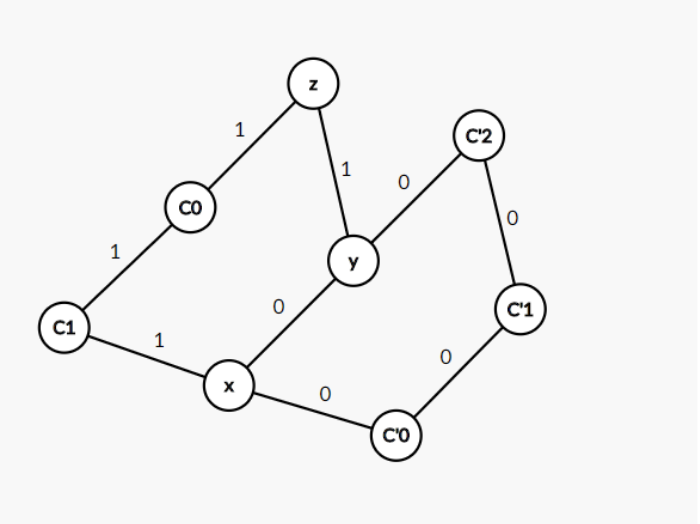
After step [3]:

 
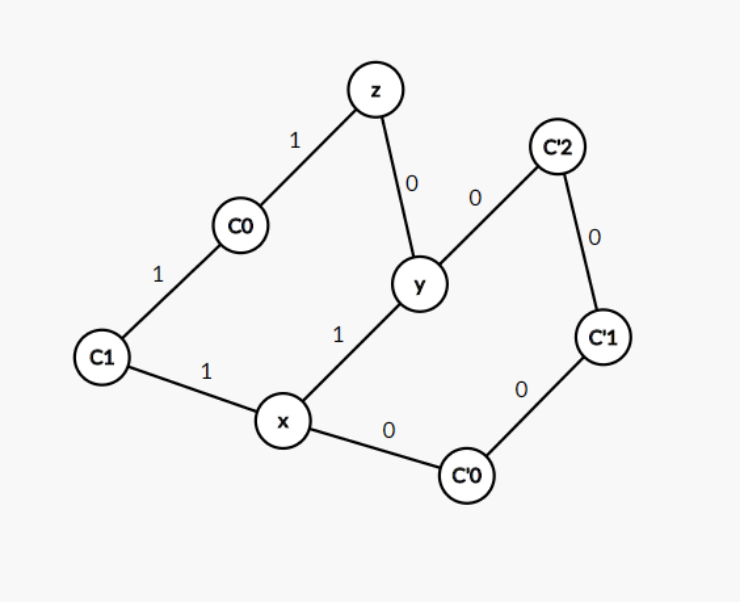
Note that x != z (since C has length at least 3). Colouring e’ from 1 to 0 can create a 0-colour cycle only if there is a path consisting only of 0-colour edges between y and z while excluding the edge e’ itself. Yet y is still connected by a 0-color path to x after step [3] (why? Because of step [3], and no other edges on this cycle were modified), and it’s impossible to get a path from z to y, since such a path would need to connect to some node in C’, which is not possible due to 3-regularity and (*)).
This completes the proof, and the algorithm runs in linear time. Here is a Java implementation of this approach:

public class ColoringEdgesDiv1 {
	static final int maxn = 1024;
	int n, m;
	boolean[][] chk, color, flipped;
	int[][] nei, deg; // (n+1) * 4, (n+1)*2
	int[] nn; // n+1
	Map<Pair<Integer, Integer>, Integer> next_flip;
	List<Pair<Integer, Integer> > ec, to_flip;
	void init_color(int x) {
		for(int i = 0; i < nn[x]; i++) {
			int y;
			if(x == n) y = i;
			else y = nei[x][i];
			if(chk[x][y]) continue;
			chk[x][y] = true;
			chk[y][x] = true;
			init_color(y);
			ec.add(new Pair(y, x));
			// ec.push_back(make_pair(y, x));
		}
	}
	void init_graph(int[] x, int[] y) {
		nei = new int[n][];
		for(int i = 0; i < n; i++) nei[i] = new int[4];
		nn = new int[n+1];
		for(int i = 0; i < m; i++) {
			nei[x[i]][nn[x[i]]++] = y[i];
			nei[y[i]][nn[y[i]]++] = x[i];
		}
		for(int i = 0; i < n; i++) {
			nei[i][nn[i]++] = n;
		}
		nn[n] = n;
	}
	void dfs(int x, boolean c) {
		for(int i = 0; i < nn[x]; i++) {
			int y = nei[x][i];
			if(color[x][y] != c || chk[x][y]) continue;
			chk[x][y] = true;
			chk[y][x] = true;
			dfs(y, c);
		}
	}
	void flip_color(boolean flag) {
		chk = new boolean[n+1][];
		for(int i = 0; i <= n; i++) chk[i] = new boolean[n+1];
		for(int i = 0; i < n; i++) {
			for(int j = 0; j < 2; j++)
				if(deg[i][j] == 1)
					dfs(i, j == 1);
		}
		to_flip = new ArrayList<Pair<Integer, Integer>>();
		if(flag) next_flip = new HashMap<Pair<Integer, Integer>, Integer>();
		for(int i = 0; i < n; i++) {
			for(int j = 0; j < 2; j++) { // 0 = false, 1 = true
				if(deg[i][j] != 2) continue;
				for(int k = 0; k < nn[i]; k++) {
					int y = nei[i][k];
					if(chk[i][y] || color[i][y] != (j==1)) continue;
					List cyc = new ArrayList();
					int x = i;
					boolean moved = true;
					while(moved) {
						cyc.add(x);
						moved = false;
						for(int l = 0; l < nn[x]; l++) {
							int z = nei[x][l];
							if(!chk[x][z] && color[x][z] == (j==1)) {
								chk[x][z] = true;
								chk[z][x] = true;
								x = z;
								moved = true;
								break;
							}
						}
					}
					cyc.remove(cyc.size()-1);
					if(flag) {
						to_flip.add(new Pair(cyc.get(0), cyc.get(1)));
						next_flip.put(new Pair(cyc.get(0), cyc.get(1)), cyc.get(2));
						next_flip.put(new Pair(cyc.get(1), cyc.get(0)), cyc.get(cyc.size()-1));
					} else {
						for(int l = 0; l < cyc.size(); l++) {
							int p = cyc.get(l), q = cyc.get((l+1)%cyc.size());
							if(flipped[p][q]) {
								to_flip.add(new Pair(p, q));
								int r = next_flip.get(new Pair(p, q));
								to_flip.add(new Pair(q, r));
								break;
							}
						}
					}
					break;
				}
			}
		}
		flipped = new boolean[n][];
		for(int i = 0; i < n; i++) flipped[i] = new boolean[n];
		for(Pair<Integer, Integer> ee : to_flip) {
			int x = ee.getKey(), y = ee.getValue();
			boolean cc = color[x][y];
			deg[x][cc ? 1 : 0]--; deg[x][cc ? 0 : 1]++;
			deg[y][cc ? 1 : 0]--; deg[y][cc ? 0 : 1]++;
			color[x][y] = !cc;
			color[y][x] = !cc;
			flipped[x][y] = true;
			flipped[y][x] = true;
		}
	}
	public int[] findColoring(int n, int[] x, int[] y) {
		this.n = n;
		m = (n*3) / 2;
		init_graph(x, y);
		ec = new ArrayList<Pair<Integer, Integer>>();
		chk = new boolean[n+1][];
		for(int i = 0; i < n+1; i++) chk[i] = new boolean[n+1];
		color = new boolean[n][];
		for(int i = 0; i < n; i++) color[i] = new boolean[n];
		init_color(n);
		// sanity check and color.
		deg = new int[n+1][];
		for(int i = 0; i < n+1; i++) deg[i] = new int[2];
		for(int i = 1; i < ec.size(); i++) if(!ec.get(i-1).getValue().equals(ec.get(i).getKey())) throw new RuntimeException(String.format("(%d, %d) -> (%d, %d)",
					ec.get(i-1).getKey(), ec.get(i-1).getValue(),
						ec.get(i).getKey(), ec.get(i).getValue()
					));
		for(int i = 0; i < ec.size(); i++) { int xx = ec.get(i).getKey(), yy = ec.get(i).getValue(); if(xx != n && yy != n) { color[xx][yy] = (i%2==1); color[yy][xx] = (i%2==1); deg[xx][i%2]++; deg[yy][i%2]++; if(deg[xx][i%2] >= 3 || deg[yy][i%2] >= 3) throw new RuntimeException();
			}
		}
		for(int i = 0; i < n; i++) nn[i] = 3;
		flip_color(true);
		flip_color(false);
		int[] ans = new int[m];
		for(int i = 0; i < m; i++)
			ans[i] = color[x[i]][y[i]] ? 1 : 0;
		return ans;
	}
}

Solution 2

Another way to solve this problem is to solve this more generally for arbitrary graphs. We can restate this problem by finding two edge-disjoint forests of the graph that cover all edges. This is almost the same as this problem: https://en.wikipedia.org/wiki/Arboricity (or more specifically, it is the same as pseudo arboricity).
This can be solved by reducing the matroid partitioning problem, which is similar to maximum flow.
To do this, we can add edges one by one. Without loss of generality, let’s say we are adding an edge in forest 0. If this doesn’t form a cycle, then we can just add it and be done. Otherwise, this induces a path on one of the trees in forest 0. We can add this edge to forest 0, iterate through the edges on this path and remove it from forest 0 and add it to forest 1 instead (note this can go back and forth recursively). We can repeat as many times as necessary until the edge can be added (only considering each (edge, forest) pair once). Note that it will always eventually be possible to add the edge if the original graph can be split into two edge-disjoint forests (due to proof of a 2-colouring existing and the matroid partitioning algorithm).
This is illustrated by the following code python code:

class Graph:
	def __init__(self, n):
		self.par = [i for i in range(n)]
		self.g = [set() for __ in range(n)]
	def root(self, x):
		if x == self.par[x]:
			return x
		self.par[x] = self.root(self.par[x])
		return self.par[x]
	def conn(self, a, b):
		return self.root(a) == self.root(b)
	def join(self, a, b):
		if self.conn(a,b):
			return
		x = self.root(a)
		y = self.root(b)
		self.par[y] = x
		self.g[a].add(b)
		self.g[b].add(a)
	def path(self, a, b, par=-1):
		if a == b:
			return []
		for x in self.g[a]:
			if x == par:
				continue
			res = self.path(x,b,a)
			if res is not None:
				return [(a,x)] + res
		return None
class ColoringEdgesDiv1:
	def add(self, graphs, a, b, idx, seen):
		if a > b: return self.add(graphs, b, a, idx, seen)
		if (a,b,idx) in seen:
			return False
		seen.add((a,b,idx))
		if not graphs[idx].conn(a,b):
			graphs[idx].join(a,b)
			return True
		if self.add(graphs, a, b, 1-idx, seen):
			return True
		edges = graphs[idx].path(a,b)
		graphs[idx].g[a].add(b)
		graphs[idx].g[b].add(a)
		for e1,e2 in edges:
			graphs[idx].g[e1].remove(e2)
			graphs[idx].g[e2].remove(e1)
			if self.add(graphs, e1, e2, 1-idx, seen):
				return True
			graphs[idx].g[e1].add(e2)
			graphs[idx].g[e2].add(e1)
		graphs[idx].g[a].remove(b)
		graphs[idx].g[b].remove(a)
		return False
	def findColoring(self, n, x, y):
		gs = [Graph(n) for __ in range(2)]
		for a,b in zip(x,y):
			assert self.add(gs, a, b, 0, set())
		ret = []
		for a,b in zip(x,y):
			if a in gs[0].g[b]:
				ret.append(0)
			else:
				ret.append(1)
		return ret

This as written, is O(E^3) in the worst case theoretically (though it is hard to make it reach the worst case). This can be sped up to O(n^2) if we didn’t iterate through used edges in the pathfinding which can be done by storing the pointer of highest edge that is still unused at each iteration. It may be possible to break this solution with a carefully constructed test case. Note that this approach does not take advantage of the fact that the graph is 3-regular, just that it can be split into two colours (it can also be modified to detect whether such a 2-colouring is possible by seeing if the code raises an assertion error)

Solution 3

Actually, the two above solutions are overkill. It is possible to solve this by using DFS to find an arbitrary forest. Edges in the forest are colored 0, otherwise, they are colored 1.
To prove this work, obviously, there are no cycles in the 0 edges, so it suffices to show there can’t be any cycles in 1 edges. Since the graph is 3-regular, the only possible way we can get a cycle in the 1 edges is on the nodes that use only at most 1 zero edge. This happens to be the leaves of our DFS tree. However, it’s impossible for the leaves to form a cycle of unused edges, otherwise, our DFS would have visited them earlier.
This leads to a short solution (in C++):

#include <bits/stdc++.h>
using namespace std;
class ColoringEdgesDiv1 {
	void dfs(int cur, vector< vector< pair<int, int > > > & graph, vector & vis, vector & ans) {
		for (auto p : graph[cur]) if (!vis[p.first]) {
			vis[p.first] = true;
			ans[p.second] = 1;
			dfs(p.first, graph, vis, ans);
		}
	}
public:
	vector findColoring(int n, vector x, vector y) {
		vector< vector< pair<int, int> > > graph(n);
		for (int i = 0; i < 3 * n / 2; i++) {
			graph[x[i]].push_back({y[i], i});
			graph[y[i]].push_back({x[i], i});
		}
		vector vis(n);
		vector ans(3 * n / 2);
		for (int i = 0; i < n; i++) if (!vis[i]) {
			vis[i] = true;
			dfs(i, graph, vis, ans);
		}
		return ans;
	}
};