July 24, 2020 Single Round Match 788 Editorials
PREFACE
This time, I challenged to problem writing in Topcoder, for the first time in my life. It was needless to say, a great experience for me. First of all, I would like to express my feeling of
appreciation to Topcoder that gave me a chance to write, publish, and let lots of contestants solve my original problems.
I made this problem set, hoping that many coders including those who are solving any of the problems whenever after the contest, could hit on like “wow, the algorithm is interesting!”. In fact, Div1 Medium – SoccerStadium, is one of my best pieces which I have come up within the first half of 2020. I hope you enjoyed the contest and/or problems.
I will conclude this SRM 788 with this editorial.
Div2 Easy – NextOlympics
This problem is in a difficult side for Div2 Easy. We need to do two things:
- First, we need to parse the string “today”. In other words, we need to get information from string “today”; values of the current year, month, and date.
- Second, from the scanned values of year, month, and date, you need to calculate how many days are remaining to July 23th, 2021, when the Tokyo Olympics begins.
In programming, there are many occasions that requires writing a complex program, but things may get simpler if you divide the procedure and think them separately. This problem is one example of it – we now divided solution of this problem into two parts, and now think them separately.
First, let’s think about the parsing part. Since the format is “YYYY-MM-DD”:
- You can get the year from 1st, 2nd, 3rd, and 4th letters.
- You can get the month from 6th and 7th letters.
- You can get the date from 9th and 10th letters.
Hence, you can retrieve them as follows, for example in C++. First step is complete!
int year = int(today[0] – ‘0’) * 1000 + int(today[1] – ‘0’) * 100 + int(today[2] – ‘0’) * 10 + int(today[3] – ‘0’);
int month = int(today[5] – ‘0’) * 10 + int(today[6] – ‘0’);
int date = int(today[8] – ‘0’) * 10 + int(today[9] – ‘0’);Now, let’s think about the second part – calculating number of days to July 23rd, 2021. You can calculate it in two ways, iteration and calculation, respectively.
Solution based on Iteration
Suppose that you can compute next day of (year, month, date). For example:
- The next day of (2020, 7, 24) is (2020, 7, 25)
- The next day of (2020, 9, 30) is (2020, 10, 1).
- The next day of (2020, 12, 31) is (2021, 1, 1).
This can be computed by using conditional statement (if-statement) like this.
- If “date” ≠ (the number of days in “month”), the next day is (year, month, date + 1).
- Else if “month” ≠ 12, the next day is (year, month + 1, 1).
- Else, the next day is (year + 1, 1, 1).
You can repeat computing it until the date becomes July 23rd, 2021. In other words, loop until (year, month, date) is (2021, 7, 23). Then, what we return will be the number of loops.
Since the oldest date given in this problem is “July 24th, 2020”, the maximum number of loops will be 364, so you can compute the answer reasonably fast.
Solution based on Calculation
Wonder if you can calculate the number of days from January 1st, year 1. In short, the number of days from “0001.01.01”. Let this value “numdays(year, month, date)”. Using this, you can easily calculate the number of days between two dates.
For this problem, the two dates are (year, month, date) and (2021, 7, 23), and you can calculate as “numdays(2021, 7, 23) – numdays(year, month, date)”.
So now, how to calculate numdays(year, month, date)? You can instantly calculate by calculation. Let’s imagine that you calculate the number of days between “0001.01.01” and “2020.07.24” by pencil and paper. You can do like this:
- There are 2019 / 4 – 2019 / 100 + 2019 / 400 = 504 – 20 + 5 = 489 leap years between year 1 and 2019. So, the total number of days in year 1, 2, 3, …, 2019 can be calculated as “365 * 2019 + 489 = 737424 days”.
- In period of January 2020 – June 2020, there are 31 + 29 + 31 + 30 + 31 + 30 = 182 days.
- There are 24 – 1 = 23 extra days in July 2020.
- Summing up all of them, numdays(2020, 7, 24) = 737424 + 182 + 23 = 737629.
That’s all! Doing the almost same thing in general, and write down it into program, you can calculate “numdays” instantly. That’s one of the ways to solve this problem.
What we need to understand
Throughout this problem, I would like to advice beginner programmers following things:
- In programming, there are many occasions that requires writing a complex program, but things may get simpler if you divide the procedure and think them separately.
- Many problems can be solved in multiple different ways or approaches. Answers are not always unique in programming world. Diversity here exists.
- If you do not come up with efficient algorithm, it is good to imagine how to solve or calculate it by hand for some example cases. In some cases, doing this can make a pathway of reaching to what algorithm is efficient enough.
Div2 Medium – StarsInTheSky
There are two kinds of solutions for this problem. I will explain both of them.
Solution #1: Brute Force All Collections
In this problem, seeing the constraints, you may spot one important thing. “N is at most 15”. Quite a small value? Definitely. Let’s think about an exponential-time algorithm.
There are 2^N – 1 possible combinations of stars. Let’s think about judging whether Mr. X can take a picture of this combination. The following examples are N = 7 and choosing 4 stars each to get into pictures. In the picture below, red stars will be chosen.
Here, the left one is “possible” and the right one is “impossible”. Think why they are.
You can see that the pictures must, at least, contain the minimum enclosing rectangle of the chosen stars. In fact, taking a picture by setting XL, XR, YL, YR for the rectangle to be the minimum enclosing rectangle of all chosen stars. That’s because, no “extra” area is there, therefore minimizing the possibility that non-chosen star comes into the picture.
For one chosen combination of stars he’d put into a picture:
- We can calculate minimum enclosing rectangle in O(N) time.
- We can judge whether the rectangle does not contain any of extra stars, by checking them if they are inside the rectangle, sequentially. It runs in O(N) time.
- It means that we can judge the possibility (true/false) of which he takes a picture, in O(N) time overall. In a word, it’s fast enough.
We need to calculate for all 2^N – 1 possible combinations. We brute-force for all of them, and count the number of which he can add into his collection. The time complexity is, formally, O(2^N × N).
When N = 15, there are 32,767 possible combinations. Some people may feel “it’s so many!” but it’s not a large value for computers, so even brute-forcing will run in a reasonably fast time. It is known that ordinary computers are capable to calculate hundreds of millions of calculations, or even billions of them, per second.
In contrast, when N becomes 60 or so, using ordinary computers, lots of years or even centuries of computation is needed. This is a scary part of exponential-time algorithm.
Implementation with “Binary Brute Force” Technique
While doing programming, it is not rare to encounter a scenario which brute-forces all 2^N possibilities, that selecting choose or not for all N things. For this, recursion is one way to implement it, but more convenient technique is there. It is called “binary brute-force”.
It is an efficient implementation to brute-force 2^N possibilities. We don’t need recursion or some advanced programming technique. For-loops are enough.
The idea of it is to brute-force k from 0 to 2^N – 1, and we see each k as a binary number. So, if N = 4, the k in the loop will be seen like 0000 🡪 0001 🡪 0010 🡪 0011 🡪 0100 🡪 0101 🡪 0110 🡪 0111 🡪 1000 🡪 1001 🡪 1010 🡪 1011 🡪 1100 🡪 1101 🡪 1110 🡪 1111, by looping through k = 0 to 15. Here, for each digit, 1 means “choose” and 0 means “not to choose”.
The i-th digit of X, in binary notation, can be calculated as (X >> i) AND 1, where “>>” is a right-shift operation and “AND” is bitwise-and. So, we can brute-force like this in C++.
for(int k = 0; k < (1 << N); ++k) {
vector<bool> choose(N);
for(int i = 0; i < N; ++i) {
if(((k >> i) & 1) == 1) choose[i] = true;
else choose[i] = false;
}
}It’s simple! Using this, we can implement StarsInTheSky, like following (in C++).
#include <vector>
#include <algorithm>
using namespace std;
class StarsInTheSky {
const int inf = 1012345678;
public:
int countPictures(int N, vector<int> X, vector<int> Y) {
int ans = 0;
for(int i = 1; i < (1 << N); ++i) {
vector<bool> chosen(N);
for(int j = 0; j < N; ++j) {
if(i & (1 << j)) {
chosen[j] = true;
}
else {
chosen[j] = false;
}
}
// step #1: finding minimum enclosing rectangle
int xl = inf, xr = -inf, yl = inf, yr = -inf;
for(int j = 0; j < N; ++j) {
if(chosen[j]) {
xl = min(xl, X[j]);
xr = max(xr, X[j]);
yl = min(yl, Y[j]);
yr = max(yr, Y[j]);
}
}
// step #2: checking part
bool ok = true;
for(int j = 0; j < N; ++j) {
if(!chosen[j] && xl <= X[j] && X[j] <= xr && yl <= Y[j] && Y[j] <= yr) {
ok = false;
}
}
if(ok) ++ans;
}
return ans;
}
};
Solution #2: Idea with Coordinate Compression
In reality, this problem is solvable in polynomial time. I will explain O(N^5) solution as an example. We use the algorithmic technique called “coordinate compression”. In this idea, literally, we compress coordinates. The example is following.
In the picture above, for example, the star numbered 9 has moved from coordinate (8, 6) to (4, 3), and the star numbered 7 has moved from coordinate (5, 5) to (3, 2).
In coordinate compression, we compress X and Y so that:
- Compress (X[0], X[1], …, X[N-1]) so that all of 0, 1, 2, …, XM will appear at least once
- Compress (Y[0], Y[1], …, Y[N-1]) so that all of 0, 1, 2, …, YM will appear at least once
In the example of picture above, XM and YM will both be 4. For any pattern, both of XM and YM will be at most N-1. So, it means, without changing positional relationships, all coordinates will become between 0 and N-1 by coordinate compression!
In this problem, it is easy to see that, the answer will not change by applying coordinate compression. That’s because positional relationship will not change. It means, after coordinate compression, you are to solve problem with following constraints:
- All of X[0], X[1], …, X[N-1] will be integers between 0 and N-1.
- All of Y[0], Y[1], …, Y[N-1] will be integers between 0 and N-1.
Apparently, the problem got easier, that we can even think about brute-forcing XL, XR, YL, YR itself. It’s actually true, because for these constraints, it is enough to choose “any of -0.5, 0.5, 1.5, 2.5, N-0.5” as XL, XR, YL, YR.
Even ignoring restriction of XL < XR and YL < YR, you can see that there are (N+1)4 possibilities for choosing (XL, XR, YL, YR). With the restriction, it gets to around a quarter of that. Since N is at most 15, it is enough to brute-force it.
However, different (XL, XR, YL, YR) may produce the same kind of picture. So, we should eliminate superfluous possibility of (XL, XR, YL, YR) that already the same kind of picture is added into collections. Since finding all-stars in the picture for each (XL, XR, YL, YR) takes O(N), this algorithm runs in O(N^5) time (or O(N^5×log(N)) time for some implementation).
Challenge for Readers
In fact, this problem can be solved in O(N^3) time. It means, even for the case with 1000 stars, it calculates the answer in just a few seconds. I think that the algorithm is as difficult as Div1 Hard problems. If you are very good at competitive programming, let’s think about it!
Div2 Hard – SquareCityWalking
This problem may not be simpler than you think. For example, some of you may have imagined a simple dynamic programming, but this is not always true: the program will fail in the following example.
Restate Problem and Solve!
Now, let’s change a problem like this. This is, in fact, equivalent to the original one.
Why are they equivalent? That’s because, GCD of K integers V[1], V[2], …, V[K], is the largest positive integer X that V[1], V[2], …, V[K] is all divisible by X. It is literally what “Greatest Common Divisor” is.
When solving problems in competitive programming, mathematics, or in some other occasions in programming, sometimes, restating problem is a good way to approach to the solution. This problem is one example of it. Having restated, the solution is clearer now!
Since the culture value A[i] is at most 100, the value of X will always be between 1 and 100. It means we can brute-force X all through 1, 2, 3, 4, …, 100.
When the value of X is already determined, each cell is “possible to pass” or “impossible to pass”. The district (x, y) is “possible to pass” if A[x*N+y] is divisible by X. There are, in reality, no other conditions.
Now, this problem has just turned into problem to reachability. Given each cell’s state, nothing or obstacle, we need to figure out whether we can advance from (0, 0) to (N-1, N-1) in shortest route. This can be solved by Depth First Search or Dynamic Programming, and the time complexity is O(N^2) for both implementations.
Since X is between 1 and max(A), the time complexity of the algorithm is O(N^2 × max(A)), which is fast enough for N = 25 and max(A) = 100.
Searching for the Faster Solution
In fact, this problem can be solved faster. That’s because, the only candidate of X is divisors of A[0]. That’s because you always pass district (0, 0).
The number of divisors d(k) of an integer k is not so large. For example:
- The maximum d(k) for k below 106, is 240 for k = 720720.
- The maximum d(k) for k below 109, is 1344 for k = 735134400.
- The maximum d(k) for k below 1012, is 6720 for k = 963761198400.
- The maximum d(k) for k below 1018, is 103680 for k = 897612484786617600.
The numbers which break the record of d(k) are called Highly Composite Numbers.
Since there are d(A[0]) candidates, the algorithm procedure is as follows:
- Find all divisors of A[0]. We need O(√A[0]) time to compute it.
- For all candidates of X (divisors of A[0]), solve the reachability problem. Since each problem is solved in O(N2) time, the answer is calculated in O(N2×d(A[0])) time.
Thus, we can solve SquareCityWalking in O(√A[0] + N2×d(A[0])) time. It means that we can calculate the answer in very short time, even for N ≦ 100 and A[i] ≦ 1012.
Div1 Easy – RailwayMaster
There are two solutions. One is based on greedy algorithm, and the another one is based on Minimum Spanning Tree. The first solution is simpler, but the second solution is faster.
Solution based on Greedy Algorithm
Alice can sell at most K edges. For Alice getting as much money as she can, let’s think about, for each selling operation, she sells a railway with maximum value among sellable railways. Actually, it is optimal.
Now, how to find a maximum value among sellable railways? To do this, we need to enumerate all sellable railways. If there are M railways, brute-force them, for erasing one railway from the network and find if the network is still connected or not, for each railway.
We can determine if the network is connected, by Depth-First Search. It takes O(M) time to calculate it. So, for each step, finding the optimal railway Alice sells takes O(M2) times. Since she repeats K time, we can solve this problem in this algorithm in O(K×M2) time. This is fast enough for all cases, which holds M≦100 and K≦100.
The method that, for each operation, we select the best answer for this moment, is called “greedy algorithm”. This problem is a case that greedy algorithm yields an optimal answer.
Solution based on Minimum Spanning Tree
Let’s think about the case of which K is equal to M – (N-1). In this case, when Alice sells K edges, there will be N-1 remaining edges. It means that, the network of railways after selling all K edges, will be a “tree” in a word of graph theory.
Alice maximizes the total value of sold railways. It means she minimizes the total value of remaining railways. So, when the number of remaining edges is N-1, the railway network she leaves behind will be a minimum spanning tree of the city’s railway network. We can find minimum spanning tree by using Prim’s Algorithm or Kruskal’s Algorithm, in O(M log M) time. The case of K = M – (N-1) is now solved.
As shown in picture above, let’s call “red railways” that is included in minimum spanning tree, and “blue railways” that is not in it.
Can you use this idea in general K? Yes.
Look at the example in picture above (N = 7). What if Alice saves 7 railways? And what if she saves 8 railways, or 9 railways, …? Actually, even for these cases, all red railways are included in optimal answer.
The only condition the railway network should hold is “to be connected”, and adding railways in minimum spanning tree into “non-selling railway list”, the connectivity condition will always hold. It means, Alice can take blue railway arbitrarily without any conditions.
So, it means, what Alice will sell is, the K highest-valued railways which is colored in blue. We can get the answer by sorting, in O(M log M) time.
Even Faster Solution!
Theoretically, this problem can be solved in O(N log N + M) time. We need to know some theoretical side of algorithm, to come up with this solution. Let’s think about it!
Div1 Medium – SoccerStadium
Did you enjoy this problem? It’s one of the most favorite problem among which I created in 2020. Hope you enjoyed it!
The game areas in soccer stadium should be all rectangular. Conversely, there should be no non-rectangular soccer stadium. So, what is the condition to be non-rectangular?
Let’s see this picture. The left one is rectangular, and the right one is non-rectangular.
You can see that rectangular area has no vertex with inner-angle of 270 degrees, but some vertices in non-rectangular area have inner-angles of 270 degrees each. This is always true because of three reasons:
- The number of vertices is 4 if rectangular, and 5 or more if non-rectangular
- The inner-angles of each vertex is either 90 degrees or 270 degrees
- If there are V vertices, the sum of inner-angles is (V-2)×180 degrees
So, the condition for all areas to be rectangular without extra edges is following:
- There is no vertex of 270 degrees.
- There are no extra nets.
Actually, this can be restated to a simple condition for each intersection of cells (we call simply “intersection” from now). That is, if there’s a vertex of 270 degrees, the net in this intersection is L-shaped. So, there should be no L-shaped intersection.
What about second condition? There are extra nets if there’s an intersection with only one net incident to it. That’s all.
Let’s gather them all. For each intersection, there are 2^4 = 16 patterns of placement nets, and we can use the following 8 of them. The other 8-pattern, which is “L-shaped” or “with only one net” are, in short, prohibited.
You can see that, for prohibited 8 patterns, there’s only one option: to remove all nets incident to it. It means that, while there are some intersections with prohibited net configuration, you should repeat removing them all. When all intersection became okay, it becomes a good soccer stadium for the first time!
You can see that the soccer stadium given by this is “maximal”, which means, for any good soccer stadium, the nets in this only includes nets in this (maximal) soccer stadium. Additional nets cannot appear for any case.
Given that, if we remove some nets, the number of game areas will only decrease. It means, to maximize the number of game areas, we should not remove nets from the maximal state!
Now, the optimal answer to “how to remove nets” is solved. Since we need to check the state of all intersection for one iteration, and there can be up to H×W iterations, the time complexity to find the maximal state is O(H^2×W^2).
We can improve the time complexity to O(H×W) with Breadth-First Search, using the fact that state of intersections only changes for intersections 4-adjacent to previously removed one.
There is one remaining tasks, counting the number of game areas. Of course, since this problem can be reduced to the problem finding the number of connected components of a graph, we can calculate in algorithm with Depth-First Search or Union-Find Tree.
However, there is one clever ad-hoc way to solve, which uses the fact that all game areas are rectangular-shaped. Here, I will introduce this solution.
Remember that all rectangles have four vertices of 90-degree inner angle. It means that, if there are K game areas, there will be exactly 4K “90-degree angles”.
In the picture above, counting them all, there are 40 angles of 90-degrees. From this information, we can calculate that there are 40 / 4 = 10 game areas.
Like this, when we count the number of 90-degree angles for each crossing point of cells, and let this number C, we get the number of game areas as C/4. That’s it!
In this way, implementation is easy, and the writer’s solution in Java only costs 50 lines.
Div1 Hard – ParkPlace
This is the hardest problem in SRM 788. Congratulations for those who solved it!
Prerequisites to Solve It
We need some knowledge about algorithm to solve it. Here, we denote |V| as a number of vertices in a graph, and denote E as the number of edges in a graph.
- Maximum Flow Problem
- Ford-Fulkerson Algorithm runs in O( F x|E|) time when F is the capacity of maximum flow.
- Dinic’s Algorithm runs in O(|V|^2 x |E|) times. For the graph that all edges have unit capacities, it runs in O(V^(2/3) , E^(1/2)) × E time.
- Linear Programming and Integer Programming
- Linear Programming (LP) can be solved in polynomial time, but Integer Programming (IP) cannot be solved in polynomial time (NP-hard).
- Maximum Flow Problem belongs to LP, but when all capacities are integers, in the optimal answer, the flow quantity for all edges are integers.
Solution for this Problem
This problem can be turned to following graph problem.

The necessary and sufficient condition for graphs to be “cycles” is:
- Degrees of all vertices are 2 (i.e. there are 2 edges incident to each vertex)
So, there should be two red edges incident to each vertex. It is easy to see that this is an Integer Programming problem. Let’s define
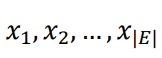
the color of edges (1 if red, otherwise 0). We need to satisfy all conditions for each vertex i:
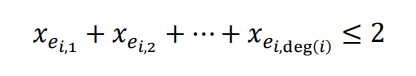
And maximizes:
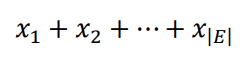
that it should be exactly N.
Please note that :
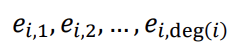
i are indices of edges incident to vertex i.
However, Integer Programming is difficult to solve. What should we do?
Actually, since we deal with a grid graph, the graph we deal with is always bipartite. In other words, we can divide vertices into two, that all edges connect two part of vertices.
Now, this is a maximum flow problem with red source and blue sink! The capacity of each edge is 1, and the capacity of each red and blue vertex is 1. We need to maximize the quantity of flow, that it will be equal to (number of vertices).
In the picture above, the bold arrows describe edges of capacity 2, and the normal arrows describe edges of capacity 1.
That’s it! If the maximum flow is less than (the number of vertices), there are no solutions. Otherwise, there is a solution according to the result of maximum flow!
There are many algorithms to solve maximum flow problem.
Ford-Fulkerson Algorithm runs in O(F×|E|) time, when F is the capacity of maximum flow. In this problem, since |F|=|V| and E ≤ 3|V|, with |V|≤ N^2 as a matter of course, it runs in O(N^4) time. It is fast enough for N ≤ 30.
On the other hand, Dinic’s Algorithm runs in O(|V|^2 x E) times. For the graph that all edges have unit capacities, it runs in 𝑂(min(𝑉 ^2/3 , 𝐸^1/2 ) × 𝐸) time time.
There are edges with capacity 2, but it is the same as adding two edges of capacity 1. Using this, it can be turned into the flow problem of |V| ≤ N^2 and E ≤ 4|V|, and all edges have unit capacities. So, it runs in O(N^3) time, which is much faster than the algorithm with Ford-Fulkerson algorithm!
Postscript
Thank you for participating, solving, or seeing this editorial! I hope that I can continue problem writing of SRM. For me, it’s the first time to write problems for TopCoder SRM, but my problem writing experience in entire competitive programming starts in 4.5 years ago, when I was 13 years old.
Thanks to a lot of people who gave me advice about problem writing, my skill grew up so much that it reached to the line that is capable of writing a TopCoder SRM contest. Here I would like to thank all of them!
square1001
Guest Blogger


