January 18, 2018 Single Round Match 724 Editorials
Some of the SRM 724 Editorials are now published. Thanks to square1001 for contributing to the editorials. If you wish to discuss the problems or editorials you may do it in the discussion forum here.
SRM 724 Round 1 – Division II, Level One – GravityPuzzleEasy – by square1001
Simple Explanation of Problem
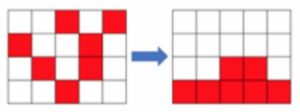
There is a board which is an H by W grid. You are given state of the grid, board. This argument consists from H strings of length W. There is a box in a cell which is in y-th topmost row and x-th leftmost column, if and only if x-th letter of y-th string of board is ‘#’. This board has the gravity, so if there are k boxes on x-th leftmost column, k bottommost cells on this column has a box and others are not. You can see the example of the right (only the red cells has a box.)
Solution and Approach
First, you have to count the number of boxes in x-th left column. It means that we have to count “the number of ‘#’ in board[y][x]” for each x. (Let this ccntt[x] for each x.)
After that, you have to get the answer. For doing this, first you have to prepare H string with length W (let this ans), and all of them should be filled with ‘.’. And then, for each x, you have to assign ‘#’ to ans[H – cnt[x]][x], ans[H – cnt[x] + 1][x],…, ans[H – 1][x].
That’s all.
Time Complexity: O(HW)
Memory Complexity: O(HW)
Source Code in C++
#include <bits/stdc++.h>
using namespace std;
class GravityPuzzleEasy {
public:
vector<string> solve(vector<string> board) {
int H = board.size(), W = board[0].size();
vector<int> cnt(W);
for (int i = 0; i < W; i++) {
for (int j = 0; j < H; j++) {
if (board[j][i] == '#') {
cnt[i]++;
}
}
}
vector<string> ans(H, string(W, '.'));
for (int i = 0; i < W; i++) {
for (int j = H - cnt[i]; j < H; j++) {
ans[j][i] = '#';
}
}
return ans;
}
};
Related Problems
SRM 724 Division 1 Medium GravityPuzzle – The problem is in same competition and the problem name is similar, but the problem is completely different. If you are good at competitive programming you can try this problem.
SRM 724 Round 1 – Division II, Level Two – OrAndSumEasy – by square1001
Simple Explanation of Problem
For a given pairOr and pairSum, determine if there is a pair of non-negative integers (a, b) such that “a + b = pairSum” and “the bitwise or of a and b is pairOr”.
For example, if pairOr= 7 and pairSum= 11, (a, b) = (5, 6) satisfies the condition. But if pairOr= 7 and pairSum= 24 there are no such (a, b) that satisfies the condition.
The value of pairOrand pairSumis between 0 and 1018.
Solution and Approach
Let “x AND y” the bitwise and of x and y, and let “x OR y” the bitwise or of the same. One key observation is, for every non-negative integer x and y, (x AND y) + (x OR y) = x + y stands.
Why this is always true? Assume if both x and y is 0 or 1.
| (x, y) | x AND y | x OR y | x + y |
| (0, 0) | 0 | 0 | 0 |
| (0, 1) | 0 | 1 | 1 |
| (1, 0) | 0 | 1 | 1 |
| (1, 1) | 1 | 1 | 2 |
As you can see from this table, if both x and y is 0 or 1, it is always
(x AND y) + (x OR y) = x + y
You can expand to all non-negative integers. For this, let’s use binary notation! Let p the k-th digit (in binary notation) of x and let q the k-th digit (in binary notation) of y. (x AND y) is the sum of (pΛq)x2k and (x OR y) is the sum of (pVq)x2k , and (x + y) is the sum of (p+q)x2k. Therefore, (x + y) – (x AND y) – (x OR y) equals the sum of ((p+q)-(pΛq)-(pVq))x2k=0x2k=0 (since both p and q is 0 or 1, (p + q) – (p AND q) – (p OR q) is always true). Since (x + y) – (x AND y) – (x OR y) = 0, it is obvious to say (x AND y) + (x OR y) = (x + y).
Now, you can reduce to this problem: Is there a pair of non-negative integers (a, b) that satisfies (a AND b) = pairAnd = (pairSum – pairOr) and (a OR b) = pairOr? (For the constraints of problem, pairAnd can be negative)
You can determine if there is (a, b), by using three following checking conditions.
1. If pairAnd is negative, obviously there is no (a, b) because (a AND b) is always non-negative.
2. If there is a non-negative integer k that k-th digit (in binary notation) of pairAnd is 1 and k-th digit (in binary notation) of pairOr is 0, there is no (a, b). You can see that in the table on up has no (x AND y, x OR y) = (1, 0) combination.
3. Otherwise, the answer always exists because you can set (a, b) = (pairAnd, pairOr).
You can determine if condition b satisfies, with judging for each bit. But there are more elegant way. If you pass condition a, you can judge only from setting (a, b) = (pairAnd, pairOr) and check if it is a valid solution.
If you use this way, you can write the code simply and can reduce the time complexity to O(1).
Useful Concepts
If you come across the problem which uses bitwise operations, think about the solution that you can divide the problem into one digit in binary notation. If you can do this the problem will be much simple.
Also, if you want to learn more about problem which uses bitwise operations, see this article – A Bit of Fun: Fun with Bits.
Source code in C++
#include <bits/stdc++.h>
using namespace std;
class OrAndSumEasy {
public:
string isPossible(long long a, long long b) {
return b - a >= 0 && ((b - a) | a) == a ? "Possible" : "Impossible";
}
};
Related Problems
SRM 724 Division 1 Easy – OrAndSum, the harder version of this problem, which is in Division 1 of the same contest.
SRM 724 Round 1 – Division I, Level One – OrAndSum – by square1001
Simple Explanation of Problem
You are given two arrays of non-negative integers of length n, pairOrand pairSum. Determine if there is a way to construct a sequence of non-negative integers of length n+1, x0,x1,x2…,xn , that satisfies xiVxi+1=pairOr[i] and xi+xi+1=pairSum[i], for all integer i (0 ≤ i < n). Here, OR denotes the bitwise or. You can assume that n is between 1 and 50, and each element of pairOrand pairSumis between 0 and 1018.
Solution and Approach
Let “x AND y” the bitwise and of x and y, and let “x OR y” the bitwise or of the same. One key observation is, for every non-negative integer x and y, (x AND y) + (x OR y) = x + y stands.
Why this is always true? Assume if both x and y is 0 or 1.
| (x, y) | x AND y | x OR y | x + y |
| (0, 0) | 0 | 0 | 0 |
| (0, 1) | 0 | 1 | 1 |
| (1, 0) | 0 | 1 | 1 |
| (1, 1) | 1 | 1 | 2 |
As you can see from this table, if both x and y is 0 or 1, it is always
(x AND y) + (x OR y) = x + y
You can expand to all non-negative integers. For this, let’s use binary notation! Let p the k-th digit (in binary notation) of x and let q the k-th digit (in binary notation) of y. (x AND y) is the sum of (pΛq)x2k and (x OR y) is the sum of (pVq)x2k , and (x + y) is the sum of (p+q)x2k . Therefore, (x + y) – (x AND y) – (x OR y) equals the sum of ((p+q)-(pΛq)-(pVq))x2k=0x2k (since both p and q is 0 or 1, (p + q) – (p AND q) – (p OR q) is always true). Since (x + y) – (x AND y) – (x OR y) = 0, it is obvious to say (x AND y) + (x OR y) = (x + y).
Now you can reduce to this problem. You are given two arrays of non-negative integers of length n, pairAnd and pairOr. Determine if there is a way to construct a sequence of length n+1, x0,x1,x2,….xn that satisfies xiΛxi+1=pairAnd[i](¿pairSum[i]-pairOr[i]) and xiVxi+1 = pairOr[i] .
The condition is only with bitwise operation! Now you can consider each digit in binary notation independently. It means the sequence x exists if and only if sequence x exists when you only consider about k-th (0-origin) digit, for all non-negative integer k.
It means you can reduce the problem that the elements of pairAnd and pairOr is 0 or 1. The problem is much simple now!
You can use greedy technique to solve. First, decide the value x0 . Repeat this until all element of x is decided: Suppose if x0,x1,x2,…..,xk is decided. Now, if pairAnd[k] = 1 and pairOr[k] = 0, obviously there is no valid sequence x. Otherwise, you can divide into three conditions:
1. Case of pairAnd[k] = 0 and pairOr[k] = 0. If xk=1, there is no valid sequence x. Otherwise, xk+1=0.
2. Case of pairAnd[k] = 0 and pairOr[k] = 1. xk+1=1-xk stands.
3. Case of pairAnd[k] = 1 and pairOr[k] = 1. If xk=0, there is no valid sequence x. Otherwise, xk+1=1.
You can determine whether there is a valid sequence x, in time complexity O(n). Since there are no more than 60 bits (≤ log2 pairAnd[k], ≤ log2 pairOr[k]), you can solve this problem efficiently, which is much faster than time limit.
Time Complexity: O(n log2 max) when max is the maximum among pairSum.
Memory Complexity: O(n)
Useful Concepts
If you come across the problem which uses bitwise operations, think about the solution that you can divide the problem into one digit in binary notation. If you can do this the problem will be much simple.
Also, if you want to learn more about problem which uses bitwise operations, see this article – A Bit of Fun: Fun with Bits.
Source code in C++
class OrAndSum {
public:
string isPossible(vector<long long> b, vector<long long> s) {
int n = s.size();
vector<long long> a(n);
for(int i = 0; i < n; i++) {
a[i] = s[i] - b[i];
if((a[i] | b[i]) != b[i]) return "Impossible";
}
for(int i = 0; i < 60; i++) {
vector<int> p(n);
for(int j = 0; j < n; j++) {
if(a[j] & (1LL << i)) p[j] = 2;
else if(b[j] & (1LL << i)) p[j] = 1;
else p[j] = 0;
}
bool flag = false;
for(int j = 0; j < 2; j++) {
int cur = j; bool f = true;
for(int k = 0; k < n; k++) {
if(cur == 0 && p[k] == 2) {
f = false; break;
}
if(cur == 1 && p[k] == 0) {
f = false; break;
}
if(p[k] == 1) cur = 1 – cur;
}
if(f) flag = true;
}
if(!flag) return "Impossible";
}
return "Possible";
}
};
Related Problem
SRM 724 Division 2 Medium – OrAndSumEasy – the easier version (n=1 version) of this problem.
Aditya
Marketing Content Manager


