December 10, 2017 Single Round Match 723 Editorials

Some of the SRM 723 Editorials are now published. Thanks to nitish_ and kapillamba4  for contributing to the editorials. If you wish to discuss the problems or editorials you may do it in the discussion forum here.
SRM 723 Round 1 – Division II, Level Two TopXorerEasy & SRM 723 Round 1 – Division I, Level One  – TopXorer – by nitish_
To obtain the answer, we will set all the bits one by one starting from maximum bit.
Suppose integers X = 1xxxxxxxxxxxx (13 bits including 1) and Y = 1xxxxxx . It can be guaranteed that we can at least obtain 111111111111 (12 bits) as the maximum XOR of these numbers. Now, in order to obtain a number greater than this, ee should make use of 13th (1) set bit of X. But when we use that bit, it is not guaranteed that all the bits after that are set to be 1.
Thus, in order to check that, we should use the set bit from the smallest available number with us. If there is a number which can contribute to that bit, then use that number. Other numbers which are greater than the smallest number can now be updated to (2^(log2(n)) – 1), because this number will have all the bits as 1 which can be utilised later.
Implementation (Div II Medium):

#include <bits/stdc++.h>
using namespace std;
class TopXorerEasy {
public:
    int maximalRating(int A, int B, int C) {
        int res = 0;
        int idx = -1;
        vector <int >v;
        v.push_back(A);
        v.push_back(B);
        v.push_back(C);
        for(int i =30; i >=0; --i)
        {
            idx = -1;
            for(int j = 0; j < 3; ++j)
            {
                if(v[j]&(1<<i))
                {
                    if(idx == -1 or v[j] < v[idx])
                        idx = j;
                }
            }
            if(idx != -1)
            {
                res += (1<<i);
                v[idx] ^= (1<<i);
                for(int j = 0; j < 3; ++j)
                {
                    if(v[j]&(1<<i))
                        v[j] = (1<<i) - 1 ;
                }
            }
        }
        return res;
    }
};

Implementation for Div I Easy is similar: we take a vector instead of three numbers A, B, C.

SRM 723 Round 1 – Division II, Level Three – SimpleMazeEasy  by  kapillamba4
There are 5n^2 rooms and order of n^4 pairs of distances to add up. The maximum distance between any two pairs can be 4*n-2 (can be observed easily)
Therefore, the answer must be some constant multiplied by n^5 and some lower degree terms (a quintic polynomial).
We can calculate the answer for several test cases using a slow brute force solution:
n = 0, result = 0
n = 1, result = 16
n = 2, result = 600
n = 3, result = 4680
n = 4, result = 19904
n = 5, result = 61000
n = 6, result = 152136
n = 7, result = 329280
These data points seem to form a nice polynomial.

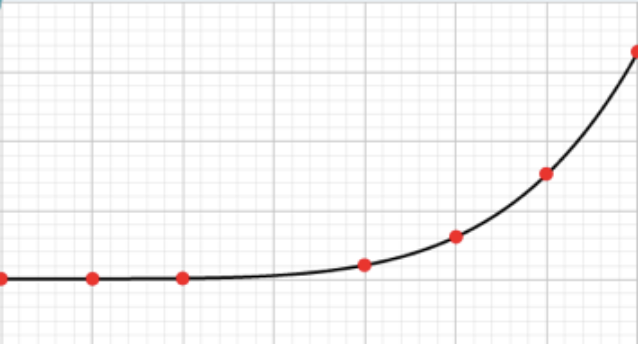
We can use Lagrange interpolation method to calculate results for other data points. We must also calculate modular multiplicative inverse of denominators for each each term in Lagrange’s interpolation formula.
We can calculate exact polynomial equation using Newton’s Interpolation Formula which comes out to be:
f(x) = 333333332*(x^3) + 666666691*(x^5)
C++Code:

#include <bits/stdc++.h>
class SimpleMazeEasy {
  const long long mod = 1000000007;
  public:
  long long power(long long base, int exp) {
    base %= mod;
    if(exp == 1) return base;
    if(base == 0) return 0LL;
    if(base == 1) return 1LL;
    if(exp == 0) return 1LL;
    if(exp % 2) return (power((base*base)%mod, exp/2)*base)%mod;
    else return power((base*base)%mod, exp/2);
  }
  int findSum(long long n) {
    return  ((333333332LL*power(n, 3))%mod + (666666691LL*power(n, 5))%mod)%mod;
  }
};

SRM 723 Round 1 – Division I, Level Two – BuffaloBuffaloBuffalo  by  kapillamba4
We are given a string of length ‘n’ consisting of several characters repeated multiple times and ‘?’ character repeated multiple times.
Find in how many ways a valid string of length ‘n’ can be constructed by interleaving several “buffalo” strings together where corresponding characters of valid string and given string match.
Note: The ‘?’ character in given string can match to any character of string “buffalo”
Let dp[a][b][d][e][f] be the number of ways to construct remaining valid string from indices [0 to idx], where
‘b’ is already repeated a times,
‘u’ is already repeated b times,
‘f’ is already repeated c times,
‘a’ is already repeated d times,
‘l’ is already repeated e times,
‘o’ is already repeated f times,
and a+b+c+d+e+f == n-idx.
Here a <= b <= c/2 <= d <= e <= f <= n/7 equality should always hold true and N should be a multiple of 7 (size of string “buffalo”)
A string is said to be valid/stable if above equalities hold true.

#include <bits/stdc++.h>
int dp[15][15][30][15][15][15];
class BuffaloBuffaloBuffalo {
    std::string pat;
    int maxBufalo;
    const int mod = 1000000007;
    const std::string bufalo = "bufalo";
public:
    bool stable(int C[]) {
        if (C['b'] <= C['u'] &&
            C['u'] * 2 <= C['f'] &&
            C['f'] <= C['a'] * 2 &&
            C['a'] <= C['l'] &&
            C['l'] <= C['o'] &&
            C['o'] <= maxBufalo) {
            return true;
        } else {
            return false;
        }
    }
    int solve(int C[], int idx) {
        if (idx == -1) {
            return 1;
        }
        int &ref = dp[C['b']][C['u']][C['f']][C['a']][C['l']][C['o']];
        if (ref != -1) {
            return ref;
        }
        if (pat[idx] != '?') {
            ++C[pat[idx] + 0];
            int ans = 0;
            if (!stable(C)) {
                ans = 0;
            } else {
                ans = solve(C, idx - 1);
            }
            --C[pat[idx] + 0];
            return (ref = ans);
        } else {
            int ans = 0;
            for (char c: bufalo) {
                ++C;
                if (stable(C)) {
                    ans = (ans + solve(C, idx - 1)) % mod;
                }
                --C;
            }
            return (ref = ans);
        }
    }
    int count(std::string pattern) {
        pat = pattern;
        int A[256];
        memset(A, 0, sizeof(A));
        memset(dp, -1, sizeof(dp));
        if (pat.size() % 7 != 0) {
            return 0;
        }
        maxBufalo = pat.size() / 7;
        for (char c2: pat) {
            bool flag = true;
            for (char c: bufalo) {
                if (c == c2 || c2 == '?')
                    flag = false;
            }
            if (flag) {
                return 0;
            }
        }
        return solve(A, pat.size() - 1);
    }
};