November 21, 2017 Single Round Match 721 Editorials

Some of the SRM 721 Editorials are now published. Check out the editorials of the interesting SRM 721 problems below. Thanks to erk52 , marcose18 , nitish_ , hl_a_k and  square1001  for contributing to the editorials. If you wish to discuss the problems or editorials you may do it in the discussion forum here.
SRM 721 Round 1 – Division II, Level One – FlightDataRecorder  by erk52
You are given two arrays: one contains headings in degrees (e.g., 0 is east, 90 is north, 180 is west, 270 is south), and one contains distances travelled in those headings. The goal is to calculate the final position of the airplane that followed the given headings for the given directions. For example, if you are given [0,90], [3, 4], this describes a plane that flew 3 units east, and 4 units north, resulting in a final distance of 5 from the origin.
This is a straightforward problem that relies on some simple trigonometry.  We have an array of headings, and an array of distances. All we need to do is take each heading-direction pair, convert this into an x-distance and a y-distance, and sum each of these components to find the final position of the plane.

To convert from heading-direction to 2D Cartesian coordinates, we apply a simple transformation:
x = r cos θ
y = r sin θ

In this problem, r is the distance and theta is the heading. The built-in sin and cos functions are expecting the argument in radians. So we have to multiply by a factor of pi/180 to convert our headings from degrees into radians.
Once we know the final x and y positions of the plane, finding the distance is a simple application of the Pythagorean theorem:
d^2 = x^2 + y^2
d = sqrt(x^2 + y^2)
 
Python Code:

import math
class FlightDataRecorder:
    def getDistance(self, heading, distance):
        total_x, total_y = 0,0
        for i in range(len(heading)):
            r = distance[i]
            theta = heading[i]
            total_x += r*math.cos(math.pi*theta/180)
            total_y += r*math.sin(math.pi*theta/180)
        return math.sqrt(total_x**2 + total_y**2)

SRM 721 Round 1 – Division II, Level Two – RememberWordsEasy – by marcose18
We will solve this question by bruteforce.
The possible values on day d1 will be between 0 and w1, inclusive. And for each possible value(let’s say i) where 0 <= i <= w1, possible values of words learnt on day (d1 + 1) will be i – 1, i, i + 1, because absolute difference can be atmost 1 between each consecutive days.
Now, for each combination of words learnt on day d1 and day (d1 + 1) which is nothing but (i, i – 1), (i, i), (i, i + 1), we will calculate minimum words that can be learnt in both semesters and maximum words that can be learnt in both semesters. If total words that are to be learnt in a particular semester is in between minimum and maximum for that particular semester in both cases, then we return string “Possible”. Otherwise if no combination exists, the answer is “Impossible”.
Now if words learnt on day d1 is i, then minimum possible words learnt in first semester will be i + (i – 1) + (i – 2) ……max(1, i – d1 + 1) and maximum words that can be learnt are i + (i + 1) + (i + 2) …….(i + d1 – 1). Similarly it can be calculated for the second semester.
Java Code:

import java.util.*;
import java.util.regex.*;
import java.text.*;
import java.math.*;
public class RememberWordsEasy {
   static boolean check(int i, int j, int w1, int w2, int d1, int d2) {
       long low_i = Math.min(d1, i) * 1L * (i + Math.max(1, i - d1 + 1)) / 2;
       long high_i = d1 * 1L * (i + i + d1 - 1) / 2;
       long low_j = Math.min(d2, j) * 1L * (j + Math.max(0, j - d2 + 1)) / 2;
       long high_j = d2 * 1L * (j + j + d2 - 1) / 2;
       if (w1 >= low_i && w1 <= high_i && w2 >= low_j && w2 <= high_j)
           return true;
       return false;
   }
   public String isPossible(int d1, int d2, int w1, int w2) {
       for (int i = 0; i <= w1; i++) {
           for (int j = i - 1; j <= i + 1; j++)
               if (check(i, j, w1, w2, d1, d2))
                   return "Possible";
       }
       return "Impossible";
   }
}

SRM 721 Round 1 – Division II, Level Three –  ApocalypseEasy  by  hl_a_k
The key observation of this problem is that this is a maximum bipartite matching problem.
The nodes in position will be destroyed; others nodes will be safe.
In the problem statement, we know, in each turn we can move each token at most once. During the turns each node may temporarily contain arbitrarily many tokens. At the very end, each node must again contain at most one token.
So, every node in position corresponds to some safe node. We can precalculate the matching graph, then find the maximum bipartite matching.
Code:

#include <bits/stdc++.h>
using namespace std;
#define ll long long
#define FT(i,f,t) for(int i=f;i<=t;++i) #define TF(i,t,f) for(int i=t;i>=f;--i)
#define REP(i,n) for(int i=0;i<n;++i)
#define MM(a,v) memset(a,v,sizeof(a))
#define ITR(it,ct) for(auto it=ct.begin();it!=ct.end();++it)
#define MOD 1000000007
int g[55][55];
bool bpGraph[55][55];
const int INF = INT_MAX / 2;
#define M 55
#define N 55
// A DFS based recursive function that returns true if a
// matching for vertex u is possible
bool bpm(bool bpGraph[M][N], int u, bool seen[], int matchR[])
{
    // Try every job one by one
    for (int v = 0; v < N; v++)
    {
        // If applicant u is interested in job v and v is
        // not visited
        if (bpGraph[u][v] && !seen[v])
        {
            seen[v] = true; // Mark v as visited
            // If job 'v' is not assigned to an applicant OR
            // previously assigned applicant for job v (which is matchR[v])
            // has an alternate job available.
            // Since v is marked as visited in the above line, matchR[v]
            // in the following recursive call will not get job 'v' again
            if (matchR[v] < 0 || bpm(bpGraph, matchR[v], seen, matchR))
            {
                matchR[v] = u;
                return true;
            }
        }
    }
    return false;
}
// Returns maximum number of matching from M to N
int maxBPM(bool bpGraph[M][N])
{
    // An array to keep track of the applicants assigned to
    // jobs. The value of matchR[i] is the applicant numbers
    // assigned to job i, the value -1 indicates nobody is
    // assigned.
    int matchR[N];
    // Initially all jobs are available
    memset(matchR, -1, sizeof(matchR));
    int result = 0; // Count of jobs assigned to applicants
    for (int u = 0; u < M; u++)
    {
        // Mark all jobs as not seen for next applicant.
        bool seen[N];
        memset(seen, 0, sizeof(seen));
        // Find if the applicant 'u' can get a job
        if (bpm(bpGraph, u, seen, matchR))
            result++;
    }
    return result;
}
struct ApocalypseEasy {
    int maximalSurvival(vector<int> p, vector<int> position, int t) {
        int n = p.size() + 1;
        REP(i,55)
            REP(j,55){
                g[i][j] = INF;
            }
        MM(bpGraph,false);
        REP(i,n - 1){
            g[p[i]][i+1] = g[i+1][p[i]] = 1;
        }
        REP(k,n)
            REP(i,n)
                REP(j,n){
                    g[i][j] = min(g[i][j],g[i][k] + g[k][j]);
                }
        set<int> ps(position.begin(),position.end());
        set<int> valid;
        REP(i,n){
            if(ps.find(i) == ps.end()){
                valid.insert(i);
            }
        }
        for(auto &p:position){
            for(auto &_t:valid){
                if(g[p][_t] <= t){
                    bpGraph[p][_t] = true;
                }
            }
        }
        return maxBPM(bpGraph);
    }
};

SRM 721 Round 1 – Division I, Level One –  RememberWords  by nitish_
To solve this problem, we have to be concerned about the d1-th day and (d1+1)-th day of the college semester.
The difference between the work load between these two days should be less than or equal to 1. If we are able to find a solution for this, then solution exists, otherwise not.
We will find the maximum and minimum permissible value for the day d1 and day (d1+1). Now, it it easy to see that any value can be achieved between this range (because we can increase or decrease or remain constant our value over a range). To find this, we will use binary search over the search space.
In case of finding the minimum permissible value we can assume a value which could be achieved at the end of sequence and rest of the terms before that is greater than that, thus the sum of range is given by = a*n + (n*n-1)/2 where a = last term of sequence, n = number of terms.
In case of maximum permissible value, if we want to a maximum value at the end of a sequence, then other terms before than that should decrease by one. Thus the sum of this range is given by = a*n – (n*n-1)/2. Be sure to handle the case where number of terms(i.e. “d” ) gets lower that your assumed maximum value, some of your terms of arithmetic progression will get negative. We dont want that.

#include <bits/stdc++.h>
#define ll long long
#define INF 1000000000LL
using namespace std;
class RememberWords {
public:
	ll bin_min(ll d, ll w) //d  = no. of terms, w = sum of terms
	{
		ll lo= 0LL, hi = INF, mid;
		while(hi > lo)
		{
			mid =(hi +lo)/2;
			ll sum = mid*d + d*(d-1)/2;
			if(sum < w) lo = mid +1; else hi = mid; } return lo; } ll bin_max(ll d, ll w) { ll lo = 0LL, hi = INF, mid; while(hi> lo)
		{
			mid = (hi+lo+1)/2;
			ll sum = d*mid - d*(d-1)/2;
			if(mid < d)
			{
				sum = mid*(mid+1)/2;
				if(sum < w) lo = mid; else hi = mid-1; } else { if(sum > w)
					hi = mid-1;
				else
					lo = mid;
			}
		}
		return lo;
	}
	string isPossible(int d1, int d2, int w1, int w2) {
	ll min1,min2,max1,max2;
	min1 = bin_min(d1,w1);
	max1 = bin_max(d1,w1);
	max2 = bin_max(d2,w2);
	min2 = bin_min(d2,w2);
	//cout<<d1min<<" "<<d1max<<" "<<d2min<<" "<<d2max<<endl; if(min1 > max1 or min2 > max2)
		return "Impossible";
	else if(max1+1 == min2)
		return "Possible";
	else if(max2+1 == min1)
		return "Possible";
	else if(max(min1, min2) <= min(max1, max2))
		return "Possible";
	else return "Impossible";
	}
};

SRM 721 Round 1 – Division I, Level Two – GraphAndPairs  by square1001

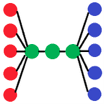
Look at the picture in above. This graph makes 25 pairs of vertices (x, y) in the which distance between vertex x and vertex y is exactly 4.
Let a be the number of red vertices, let b be the number of blue vertices, and let c be the number of green vertices.
Let’s consider the case which constructs the tree graph by adding edges, from each red vertex to the first green vertex, from each blue vertex to the last green vertex, and from the i-th green vertex to the (i+1)-st green vertex (1 ≤ i ≤ c-1).
If c ≥ 2, the distance between vertex x and vertex y is c+1 if and only if either x or y is a red vertex and another is a blue vertex. The reason is, if one is a red vertex and another is blue, the distance between x and y is c+1, and if either x or y belongs to a green vertex, the distance between x and y is less than c+1, and if x and y are both red vertices, the distance is 2 if x ≠ y and otherwise 0, and similarly if x and y are both blue vertices.
So, if you set c = d-1, the number of good pairs is ab and the number of vertices is a + b + c = + b + d – 1. Note that this statement is only established if c ≥ 2 (therefore d ≥ 3).
The case of d ≥ 3
Let √k be the floor of the square root of k.
If you set (a, b) = (√k, √k), you can make (√k)2 good pairs with 2√k + d – 1 vertices.
Now you have to make extra k – (√k)2 good pairs by making another graph as connected components. If you set (a, b) = (k – (√k)2, 1), you can make k – (√k)2 good pairs with k – (√k)2 + d vertices.
By combining the two graphs, you can make s good pairs with 2√k + k – (√k)2 + d – 1 vertices. As k ≤ 50000, the maximum value of √k is 223, and the maximum value of k – (√k)2 is 444 because it’s the difference of s and the largest square number less than or equal to k.
As d ≤ 50, the maximum number of vertices is less than or equal to 2 × 233 + 444 + 2 × 50 – 1 = 989. Since the graph is a forest, the number of edges is less than number of vertices, so it satisfies the condition of |V| ≤ 1000, |E| ≤ 1000 (|V| is the number of vertices, and |E| is the number of edges).
The case of d = 2
The constructing style of case d ≤ 3 and case d = 2 is quite different.
First, a star graph Sa = K1,a contains C(a, 2) = a(a-1)/2 vertex pairs which distance between one and another is 2.
Second, a path graph Pb contains max(b-2, 0) vertex pairs which distance between one and another is 2.
If you maximize a, you can minimize b since a ≥ 1. Let’s think about maximizing a. Solving the inequality a(a-1)/2 ≤ k, you get

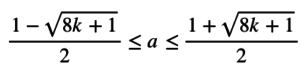
Since k ≥ 1, a = 1 is always one solution, so the maximum value of a is

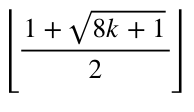
If you set (a, b) =

, the number of good pairs will be k. Since k ≤ 50000 => a ≤ 316, it follows that b ≤ ½ × 316 × 315 – ½ × 315 × 314 = 315, so the number of vertices will be less than or equal to a + b + 3 = 624. Since the graph is a forest, the number of edges is less than the number of vertices, so it satisfies the condition of |V| ≤ 1000, |E| ≤ 1000.

#include <cmath>
#include <vector>
#include <algorithm>
using namespace std;
class GraphAndPairs {
public:
	vector<int> construct(int d, int k) {
		vector<int> ret;
		if (d >= 3) {
			int sq = sqrt(k) + 1.0e-6;
			int a1 = sq, b1 = sq;
			int a2 = k - sq * sq, b2 = 1;
			for (int i = 0; i < d - 2; i++) {
				ret.push_back(i);
				ret.push_back(i + 1);
			}
			for (int i = 0; i < a1; i++) {
				ret.push_back(0);
				ret.push_back(i + d - 1);
			}
			for (int i = 0; i < b1; i++) {
				ret.push_back(d - 2);
				ret.push_back(i + a1 + d - 1);
			}
			for (int i = 0; i < d - 2; i++) {
				ret.push_back(i + a1 + b1 + d - 1);
				ret.push_back(i + a1 + b1 + d);
			}
			for (int i = 0; i < a2; i++) {
				ret.push_back(a1 + b1 + d - 1);
				ret.push_back(i + a1 + b1 + 2 * d - 2);
			}
			for (int i = 0; i < b2; i++) {
				ret.push_back(a1 + b1 + 2 * d - 3);
				ret.push_back(i + a1 + b1 + a2 + 2 * d - 2);
			}
		}
		else {
			int a = (1 + sqrt(8 * k + 1)) / 2 + 1.0e-6, b = k - a * (a - 1) / 2;
			for (int i = 0; i < a; i++) {
				ret.push_back(0);
				ret.push_back(i + 1);
			}
			for (int i = 0; i < b + 1; i++) {
				ret.push_back(i + a + 1);
				ret.push_back(i + a + 2);
			}
		}
		ret.insert(ret.begin(), *max_element(ret.begin(), ret.end()) + 1);
		return ret;
	}
};