Single Round Match 716 Editorials

SRM 716 Editorials are now published. We are still awaiting the submission to the Div I Hard problem. Thanks to survival07, Vetteru and Shizhouxing for contributing to the SRM 716 Editorials. If you wish to discuss the problems or editorials you may do it in the discussion forum here.
Want to write an editorial? And get featured on the Topcoder blog? We still have some editorials challenges open - Contribute to SRM Editorials.

 
SRM 716 Round 1 - Division II, Level One - Permutiple by survival07

Problem statement: Rearrange the digits of a number (x) without leading zeros such that new number y is a multiple of x and x != y. Check whether it’s possible.
Mathematical form of y = x*C. What is the range of C here. It can’t be 1. In that case y would become equal to x. C can’t be 10 as it would add an extra digit ‘0’ to x. So range of C is [2, 3, …, 9]
So the idea is to multiply x by all possible values of C one at a time and then check if the product y has the same number of counts for each digit (0-9) as x.
Another idea would be generating all possible permutations for digits of x and then check if any permutation is a multiple of x. In that case it needs to ensure that permutation doesn’t have leading zeros.
Here is the C++ code:
[cpp]
class Permutiple {
public:
string isPossible(int x) {
string p = "Possible";
string imp = "Impossible";
int i,j;
//count_x[i] is the counter number for digit i in number x
int count_x[10];
int a = x;
memset((count_x),(0),sizeof(count_x)); //initialize x's counter array to zero's
while(a){
count_x[a%10]++;
a /= 10;
}
forl(i,2,10){
int y = x*i;
//count_y[i] is the counter number for digit i in number y
int count_y[10];
memset((count_y),(0),sizeof(count_y)); //initialize array to zero's
while(y){
count_y[y%10]++;
y /= 10;
}
bool ok=true;
forl(j,0,10){
if(count_x[j] != count_y[j]){ //check if digit j has equal counter in both x and y
ok=false;
break;
}
}
if(ok) //return 'Possible' if both counter arrays are same
return p;
}
return imp; //Otherwise 'Impossible'
}
};
[/cpp]
 
 
SRM 716 Round 1 - Division II, Level Two – ConstructLCSEasy by survival07

Important constraint in this problem is: ab ≤ bc ≤ ca
If the LCS length of two strings A and B is x, then the length of both A and B is at least x. Because LCS can’t be larger than the smallest (based on length) input string. Let’s denote length of string A as L(A).
So, from parameter ab we can say: L(A), L(B) ≥ ab
From parameter bc: L(B), L(C) ≥ bc
From parameter ca: L(A), L(C) ≥ ca
Here is the thing – if a variable x is greater than or equal to both y and z and y ≥ z, we can definitely draw a conclusion that x ≥ y. No need to consider z.
Considering the above constraints on L(A) we see L(A) ≥ ca and ab. But ca ≥ ab. So L(A) must be greater than or equal to ca. Similarly, L(B) ≥ bc and L(C) ≥ ca. From these derived constraints it’s quite intuitive to build strings A, B and C. Following picture will illustrate the process of building strings.

Here we see that f(A,B) [LCS of A and B] = ab as there are ab 1’s in B and ab ≤ ca.
F(B,C) = bc because string C includes B and L(B) = bc. Number of 1’s in C = ab+ (ca-ab) = ca which makes f(C,A) = ca. Simultaneously swapping all 1’s to 0’s and all 0’s to 1’s in string A, B and C will build a different solution. Here is the C++ code:
[cpp]
class ConstructLCSEasy {
public:
string construct(int ab, int bc, int ca) {
string A = string(ca,'1');
string B = string(ab,'1') + string(bc-ab,'0');
string C = B + string(ca-ab, '1');
return A + " " + B + " " + C;
}
};
[/cpp]
 
 
 
SRM 716 Round 1 - Division II, Level Three - JumpDistancesOnTreeEasy by Vetteru

The solution of this problem consists of 3 parts such as initialize, evaluate and update.
In initialize section (void init(int[] p) in my code), we have to initialize some variable and calculate minimum distances of all pairs.
To calculate minimum distances, I used Warshall–Floyd Algorithm.
In evaluate section (boolean next(int dist) in my code), we have to evaluate the next step is possible or impossible.
If a node that is S[i] (i = current index) distance away from reachable nodes exists, the step is possible. otherwise, impossible.
In update section (void update(int dist) in my code), we have to update reachable nodes.
New reachable node is a node that is n distance (any combination of previous used distances) away from current reachable nodes.
Example of the solution:
distance set S = [2, 4]

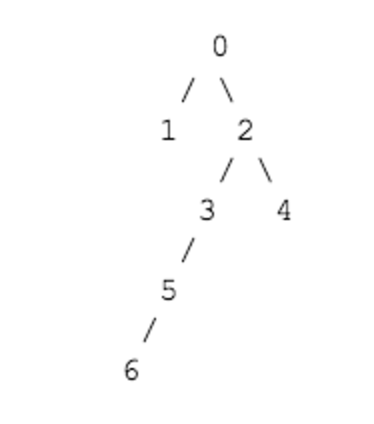
initialize : Initialize variables and calculate distance of all pairs.
evaluation : First, we are at '0' and a given distance is 2. We can reach '3' and '4'. So the evaluation returns possible.
update : Current reachable node is only '0'. So we add all nodes that distance is multiple of 2.
Note that given distance is a form of set, so we can use that distances many times.
In this time '3', '4' (distance : 2), '6' (distance : 4) are reachable.
So at the end of this section, reachable nodes will be ['0', '3', '4', '6'].
evaluation : In this time, we can be at ['0', '3', '4', '6'] and a given distance is 4.
'0' is 4 distance away from '6'. So this evaluation also returns possible.
update : In this update section, No new reachable nodes found.
finish : Every queries are done correctly and the answer is "POSSIBLE".
Complexity:
n := the number of vertexes
s := the size of set of distances
initialize : Time - O(n^3), Space - O(n^2)
- Warshall–Floyd Algorithm's cost
- initialize 2D array that hold all distances of all paris.
evaluate : Time - O(n^2), Space - O(1)
- In worst case, we have to check all distances of all pairs.
- No memory required.
update : Time - O(n^2), Space - O(n)
- In worst case, we have to check all distances of all pairs.
- Need a list that hold reachable nodes.
total : Time - O(n^3) or O(s x n^2), Space - O(n^2)
- We call initialize only one time, evaluate s times, and update s times.
In this problem, s and n is same size (1 <= s, n <= 50). So the time complexity is O(n^3) or O(s x n^2).
- Space complexity is O(n^2). A 2D array that hold all distances of all paris is that.
[java]
import java.util.HashSet;
import java.util.Set;
public class JumpDistancesOnTreeEasy {
private static final int INF = 1<<25;
private int size;
private int[][] distances;
private Set<Integer> selectableDist;
private Set<Integer> selectableNode;
public String isPossible(int[] p, int[] S) {
init(p);
for (int s : S) {
boolean isPossible = next(s);
if (!isPossible) {
return "Impossible";
}
update(s);
}
return "Possible";
}
private void init(int[] p) {
size = p.length + 1;
distances = new int[size][size];
for (int i = 0; i < size; i++)
for (int j = 0; j < size; j++)
distances[i][j] = i == j ? 0 : INF;
for (int i = 0; i < p.length; i++) {
distances[i+1][p[i]] = distances[p[i]][i+1] = 1;
}
for (int k = 0; k < size; k++)
for (int i = 0; i < size; i++)
for (int j = 0; j < size; j++)
distances[i][j] = Math.min(distances[i][j], distances[i][k] + distances[k][j]);
selectableDist = new HashSet<>();
selectableNode = new HashSet<>();
selectableNode.add(0);
}
private boolean next(int dist) {
for (int node : selectableNode) {
for (int i = 0; i < size; i++) {
if (distances[node][i] == dist) {
return true;
}
}
}
return false;
}
private void update(int dist) {
selectableDist.add(dist);
while (true) {
Set<Integer> additionalNode = new HashSet<>();
for (int node : selectableNode) {
for (int i = 0; i < size; i++) {
if (selectableDist.contains(distances[node][i]) && !selectableNode.contains(i)) {
additionalNode.add(i);
}
}
}
if (additionalNode.isEmpty()) {
break;
}
selectableNode.addAll(additionalNode);
}
}
}
[/java]
 
 
SRM 716 Round 1 - Division I, Level One ConstructLCS by Shizhouxing

If ab<=bc<=ca, we can easily construct a solution in the following way:
(a) A has ab ones and follows by ca-ab zeros.
(b) B has bc ones.
(c) C has bc ones and follows by ca-ab zeros.
You can validate that the LCS’s between A and B, B and C, C and A are exactly ab,bc,ca respectively.
Now if ab, bc, ca given don’t satisfy ab<=bc<=ca, we can rearrange the order of A,B,C when solving the problem. For example, if ab>bc, we can make the order of strings become C,B,A. Now the LCS’s between the 1st string and the 2nd string, 2nd string and the 3rd string, 3rd string and 1st string are bc,ab,ca respectively. In this way, we’ve swapped ab and bc actually. We can do similar things for ab and ca, bc and ca. Hence we can always change the problem into the one where ab<=bc<=ca.
Code
[cpp]
#include <string>
using namespace std;
class ConstructLCS {
public:
void solve(int ab, int bc, int ca, string& a, string& b, string& c)
{
if (ab > bc)
return solve(bc, ab, ca, c, b, a);
if (ab > ca)
return solve(ca, bc, ab, a, c, b);
if (bc > ca)
return solve(ab, ca, bc, b, a, c);
a = b = c = "";
for (int k = 0; k < ab; k++)
a += '1';
for (int k = 0; k < bc; k++)
b += '1', c += '1';
for (int k = 0; k < ca - ab; k++)
a += '0', c += '0';
}
string construct(int ab, int bc, int ca)
{
string a, b, c;
solve(ab, bc, ca, a, b, c);
return a + " " + b + " " + c;
}
};
[/cpp]
 
 
SRM 716 Round 1 - Division I, Level Two JumpDistancesOnTree by Shizhouxing

We can first get distances between any two nodes by DFS starting from each node.

Now let’s consider which nodes can be chosen by Rabbit Hanako during her trip. First she must choose node 0 as she starts from city 0. Then if she has chosen node u, for another node v, if the distance between u and v is in set S, she can go to city v right after visiting u and then go back to u. So node v can also be chosen. In this way, we get all nodes that can be chosen. We may use BFS to implement it.

Next we should check whether each element in S can appear as a distance between two nodes during the trip. We need check that for each element in S, whether there are two nodes that can be chosen and the distance between them are exactly this element in S. If all elements in S satisfy the condition, it’s possible to have a required trip, otherwise it’s impossible.

Code
[cpp]#include <bits/stdc++.h>
using namespace std;
int dis[2500][2500], ok[2500], valid[2500], n;
vector<int> E[2500];
queue<int> Q;
void dfs(int u, int fa, int* dis) {
if (fa == -1) dis[u] = 0;
else dis[u] = dis[fa] + 1;
for (auto v:E[u])
if (v != fa)
dfs(v, u, dis);
}
class JumpDistancesOnTree
{
public:
string isPossible(vector <int> p, vector <int> S)
{
memset(valid, 0, sizeof(valid));
memset(ok, 0, sizeof(ok));
for (int i = 0; i < S.size(); ++i) valid[S[i]] = true;
n = p.size() + 1;
for (int i = 0; i < n; ++i) E[i].clear();
for (int i = 0; i < p.size(); ++i) E[p[i]].push_back(i + 1), E[i + 1].push_back(p[i]);
for (int i = 0; i < n; ++i)
dfs(i, -1, dis[i]);
ok[0] = true;
Q.push(0);
while (Q.size()) {
int u = Q.front(); Q.pop();
for (int v = 0; v < n; ++v)
if (valid[dis[u][v]]) {
valid[dis[u][v]] = 2;
if (!ok[v]) {
ok[v] = true;
Q.push(v);
}
}
}
for (int i = 0; i < S.size(); ++i)
if (valid[S[i]] < 2) return "Impossible";
return "Possible";
}
};
[/cpp]