May 4, 2017 Single Round Match 713 Editorials
We now have some of the SRM 713 Editorials published. We are awaiting or reviewing the submissions for some of them. If you would like to contribute an editorial for those problems you may do so by submitting to their respective challenge.
Thanks to stni, pakhandi, marcose18 , GoogleHireMe for contributing to the SRM 713 editorials.
Single Round Match 713 Round 1 – Division II, Level One SymmetryDetection by pakhandi

The problem can be solved by traversing the matrix and checking for symmetry in a greedy / ad-hoc way.
Let us first solve the problem for the vertical-symmetry.
We want to check if, for every cell [i][j], if it is equal to [i][cols – j – 1]. In this case we don’t need to visit every cell. We only need to check this condition for cells in all the rows but only half the columns. The proof of this optimization is very trivial and is left as an exercise for the reader.
For the horizontal-symmetry, we can use the same method for all the columns but half the rows, comparing [i][j] with [rows – i – 1][j].
The method is very similar to what is used for checking palindrome.
Please check the implementation below for details.
class SymmetryDetection
{
public:
string detect(vector board)
{
bool h = 1, v = 1;
int rows = board.size();
int cols = board[0].size();
for(int i = 0; i < rows; i++)
{
for(int j = 0; j <= cols / 2; j++)
{
if(board[i][j] != board[i][cols - j - 1])
{
v = 0;
}
}
}
for(int i = 0; i <= rows / 2; i++)
{
for(int j = 0; j < cols; j++)
{
if(board[i][j] != board[rows - i - 1][j])
{
h = 0;
}
}
}
if(h && v)
{
return "Both";
}
else if(h)
{
return "Horizontally symmetric";
}
else if(v)
{
return "Vertically symmetric";
}
else
{
return "Neither";
}
}
};
Single Round Match 713 Round 1 – Division II, Level Two PowerEquationEasy by marcose18
In this question we will iterate through all the values & it’s powers which are less than n.
Now we will calculate answer for a number i & it’s powers in one go . Now for some power of i, let’s assume i ^ x we have to calculate all such values where (i ^ x) ^ c = (i ^ y) ^ d such that c, d & i ^ y <= n. Now clearly x, y <= maxpow where i ^ maxpow <= n while i ^ (maxpow + 1) > n.
Also (i ^ x) ^ c = (i ^ y) ^ d implies x * c = y * d. In short (x / y) = (d / c).
So for fixed values of x, y we have to find c & d such that it satisfies above equation while it is also <= n. So to find such c & d, reduce x & y to it’s lowest form by dividing both x & y by gcd(x, y).
Now it’s easy to see that total possible values = n / max(tempx, tempy) where tempx & tempy are x / gcd & y / gcd respectively. Do the above for all values of i and add it to answer. One final thing to note here is if i > sqrt(n) then it contains no power that is less than n i.e i ^ x = i ^ y only for x = y = 1. So each of them will contribute n to the final answer and thus we will loop only upto sqrt(n) instead of n.
Below is the code of above explanation.
Here HashSet is used to keep track of visited numbers and their powers.
import java.util.*;
import java.util.regex.*;
import java.text.*;
import java.math.*;
public class PowerEquationEasy {
// Calculating gcd of two numbers.
static int gcd(int a, int b) {
if (a < b) {
int temp = a;
a = b;
b = temp;
}
if (b == 0) return a;
return gcd(b, a % b);
}
public int count(int n) {
long ans = n * 1L * n;
long mod = (long) 1E9 + 7;
ans %= mod;
HashSet set = new HashSet<>();
// Iterate through all values but not those which are stored in the hashset which are nothing but powers of earlier values and we have calculated answers for them before.
for (int i = 2; i * i <= n; i++) {
if (set.contains(i)) continue;
int maxpow = 0;
int temp = i;
while (temp <= n) {
++maxpow;
set.add(temp);
temp *= i;
}
// Find the answer for all x & y such that (i ^ x) ^ c = (i ^ y) ^ d.
for (int x = 1; x <= maxpow; x++)
for (int y = 1; y <= maxpow; y++) { int g = gcd(x, y); int tempx = x / g, tempy = y / g; ans += n / Math.max(tempx, tempy); while (ans >= mod) ans -= mod;
}
}
// All numbers greater than sqrt(n) will have no power that is less than n and for each of them there will be ‘n’ identities.
ans += (n - set.size() - 1) * 1L * n;
ans %= mod;
return (int) ans;
}
}
Single Round Match 713 Round 1 – Division II, Level Three DFSCountEasy by GoogleHireMe
In this problem, you have to calculate number of different paths to traverse the graph using depth first search.
First of all, let’s try to set the possible upper bound for the answer. There are exactly N! (n-factorial) permutations of numbers from 1 to N. All of those sequences will be valid when we have a complete graph.
So, the maximal possible answer can reach 13! = 6227020800, and this means that a brute force (trying all the possible paths) wouldn’t fit into time bounds.
To solve this problem, we can use dynamic programming.
In every dynamic programming problem you have to detect four things:
- a) define a state
- b) find a way to split the problem into subproblems
- c) define the base state: the subproblem for which you know the solution immediately, without splitting it into subproblems.
- d) find a way to combine the subproblems’ solutions to get the solution of the main problem
Let’s tackle this step by step:
a) Let’s define our problem’s state as a pair of <start_node, available_nodes>, where start_node is the node from which we start building the path, and available_nodes – set of nodes which are not yet visited. Then, to find the solution to the initial problem, we would have to sum up all solutions of subproblems with all possible start nodes when all nodes as available.
Let’s consider the following example:
node 1 is not available (since it was visited before) and start_node is 2;
State: start_node=2, available_nodes={3, 4, 5, 6, 7, 8, 9}
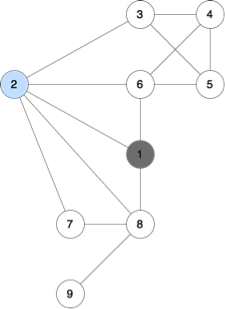
b) To split the problem into subproblems, we can just try to extend our existing path and make a one DFS call to one of the available
In the example, we can go to the next possible subproblems (2 is no longer available, start_node highlighted with blue color):
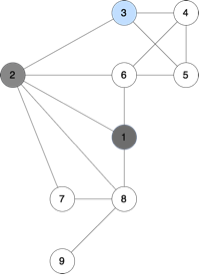
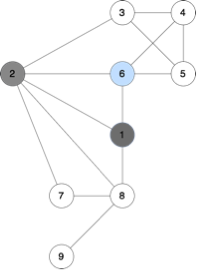
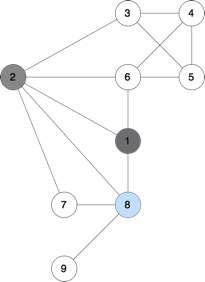
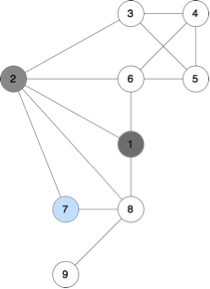
c) The base state can be the state with only one available node – it means that there is nowhere else to go, and the answer is 1 (only that node, and that’s the end).
d) Now, we have to find a way to combine the solutions to the subproblems. And this is the place where things get really interesting:
The first thing we should notice is that once we decided which child to go next, all other children that are connected (directly or via available nodes) will not be available once the dfs() will return, since they will be marked as used in one of the dfs()’s subcalls of the call on that child.
For instance, in the example above, when we call dfs for node 3 from the node 2, it will mark nodes 4, 5 and 6 as used. Thus, after the end of the call, we wouldn’t be able to call dfs for the node 6 from the node 2 anymore.
Let’s call the subset of the “reachable” nodes as the component.
In the example above, once we consider node 2 as start_node and node 1 as unavailable, we will have to components: consisting of nodes {3, 4, 5, 6} and {7, 8, 9}.
Since you can pick only one node per component to move to, the number of dfs() calls from the start_node equals to the number of components in that state.
Since the components are independent from each other, the result for the given state will be the multiplication of number of paths for all components separately.
Also, because of the independance of those components (you cannot reach one from another), we can do those above mentioned dfs() calls in any order, that means that we have to multiply the result by K! (k-factorial) where K is the number of components for the current state.
One more thing we still have to consider – what if one component contains more than one neighbour of the start_node. Since we can “enter” the component only once (after that all nodes of the component will be marked as used), the number of different paths for the component will be the sum of those subproblems with different children as start_node.
A few notes on the implementation: the recursive solution looks nice, however, to avoid solving the same subproblem multiple times, it’s important to implement this recursion with memoization of the answers for every state previously calculated. We can achieve this with map data structure.
In my solution I use breadth first search to find the components.
Also, I use the bitmask to represent available nodes instead of the set, since the number of the nodes is small, and bit operations are generally “cheaper” (in terms of performance) than the operations on the set. Here, 1 on the ith position of the binary representation of the mask variable means that the ith node is in available_nodes set.
Complexity:
Let n be equal to the number of nodes.
In the worst case, for every state (2^n * n) we will perform breadth first search ( O(n*n)) for every neighbor (n).
Thus O(2^n * n * n * n^2) = O( 2^n * n^4 )
To sum up, the solution will look like follows:
#include <string>
#include <vector>
#include <map>
#include <queue>
using namespace std;
class DFSCountEasy {
int n;
vector<string> G;
map<pair<int, int>, long long> cache;
long long f(int mask, int v) {
// Remove current node from the available nodes
mask = mask & (~(1 << v));
if (cache.count({mask, v})) {
// The solution for this subproblem was calculated before
return cache[{mask, v}];
}
map<int, long long> components;
for (int i = 0; i < n; i++) {
if (G[v][i] == 'Y' && (mask & (1 << i))) {
// BFS for child i
queue<int> q;
q.push(i);
// Bitmask for the set of nodes included in the corresponding component
int submask = 1 << i;
while (!q.empty()) {
int u = q.front();
q.pop();
for (int j = 0; j < n; j++)
if (mask & (1 << j)) {
if (G[u][j] == 'Y' && !(submask & (1 << j))) {
submask |= 1 << j;
q.push(j);
}
}
}
components[submask] += f(submask, i);
}
}
long long res = 1;
for (auto x : components) res *= x.second;
for (int i = 0; i < components.size(); i++) res *= i + 1;
return cache[{mask, v}] = res;
}
public:
long long count(vector<string> _G) {
G = _G;
n = G.size();
long long res = 0;
for (int i = 0; i < n; i++) res += f((1 << n) - 1, i);
return res;
}
};
Single Round Match 713 Round 1 – Division I, Level One PowerEquation by stni
 If a=c, b=d, we have n*n identities.
If a=c, b=d, we have n*n identities.
Here, 1^1=1^2=1^3=…=1^n,—-(n-1)
1^2=1^1=1^3=…=1^n,—-(n-1)
…
1^n=1^1=1^2=…=1^(n-1) —-(n-1)
For a=1 and b=1,
we need to add another n*n-1.
So we already have n*(2*n-1) identities obviously.
For a != c:
Without loss of generality, we say ac.
For all integers not power of other integers p,
let a=p^i, c=p^j
number of c we can choose from equals to
number of powers of least common multiple(LCM) of a and c.
j/gcd(i,j) is the min distance between powers of LCM,
n/(j/gcd(i,j)) is the number of such identities in [1..n]
multiply 2 for symmetry of a-c, b-d
Complexity is O(n)
#include<set>
using namespace std;
typedef long long ll;
const ll mod=1e9+7;
ll gcd(ll a,ll b){
return a?gcd(b%a,a):b;
}
class PowerEquation{
public:
int count(int n0){
ll n=n0;
set<ll>se; //all power bases
ll ans=n*(n*2-1)%mod;
for(ll p=2;p*p<=n;p++){
if(se.count(p))
continue; //we already calculated p's base
ll t=p;
ll k=0;//number of powers of t
while(t<=n){
se.insert(t);
t*=p;
k++;
}
for(ll i=1;i<=k;i++){
for(ll j=i+1;j<=k;j++){
ans+=n/(j/gcd(i,j))*2;
ans%=mod;
}
}
}
return (int)ans;
}
};
Single Round Match 713 Round 1 – Division I, Level Two DFSCount by stni

We have n nodes, each has n potential positions.
Complexity is O(n^2)
#include<vector>
#include<array>
#include<string>
using namespace std;
typedef long long ll;
vector<string>G;
vector<array<pair<ll,ll>, 15>>mem;
class DFSCountEasy{
public:
pair<ll,ll> dfs(ll visited, ll last){
if(mem[visited][last].second)return mem[visited][last];
pair<ll,ll> r(0,0);
for(int i=0;i<G.size();i++){
if((last!=G.size()&&G[last][i]=='N')||(visited&(1ll<<i)))continue;
pair<ll,ll>t1=dfs(visited|(1<<i), i);
pair<ll,ll>t2=dfs(t1.second,last);
r.first+=t1.first*t2.first;
r.second=t1.second|t2.second;
}
if(r.second==0){
r=make_pair(1, visited);
}
return mem[visited][last]=r;
}
ll count(vectorG){
::G=G;
mem.clear();
mem.resize(1<<G.size());
pair<ll,ll> r=dfs(0,G.size());
return r.first;
}
};
Single Round Match 713 Round 1 – Division I, Level Three CoinsQuery
We are awaiting the submission for the following editorial. If you would like to contribute an editorial for this problem you may do so by submitting to this challenge.
Harshit Mehta
Sr. Community Evangelist


