June 13, 2019 Shor's Algorithm in Quantum Computing
Shor’s Algorithm
Effective algorithms make assumptions, show a bias toward simple solutions, trade off the cost of error against the cost of delay, and take chances.” – Brian Christian, Tom Griffiths
This article will introduce Shor’s Algorithm in the Quantum Algorithms series. In the series so far, we have seen Grover’s Algorithm. The reader will learn how to implement Shor’s Algorithm by using amplitude amplification, and how to analyze the performance of the algorithm.
A computer executes the code that we write. One needs an algorithm to develop the code. Typically an algorithm is based on a problem solution. It will have a set of steps and rules to be executed in a sequence. Pseudocode is used to present the flow of the algorithm and helps in decoupling the computer language from the algorithm.
Quantum mechanics is used by the quantum computer to provide higher computer processing capability. Quantum computers will beat out supercomputers one day. Quantum computers will be used in fields such as pharma research and materials science where higher computing power is required. The classical computers will be there for providing basic solutions to the problems. Quantum computers operate on quantum bits and processing capability is in the quantum bits.
Quantum bits can get entangled, meaning two qubits can be superimposed in a single state. Modifying a quantum bit which is entangled will immediately impact the state of the other entangled quantum bit. This phenomenon occurs when the quantum bits are a distance apart. Einstein coined this phenomenon as “spooky action at a distance”. Quantum bits provide an exponential leap in the processing capability of the quantum computer.
Shor’s algorithm was invented by Peter Shor for integer factorization in 1994. This algorithm is based on quantum computing and hence referred to as a quantum algorithm. The algorithm finds the prime factors of an integer P. Shor’s algorithm executes in polynomial time which is of the order polynomial in log N. On a classical computer, it takes the execution time of the order O((log N)3). Quantum Fourier Transform is the basis of the algorithm which finds the period of the function which gives the value based on the product of the prime factors.
The code below shows a Shor’s algorithm implementation. In this implementation, we look at the prime factorisation based on Shor’s algorithm.
Prerequisites:
- You need to set up Python3.5 to run the code samples below. You can download from this link.
Problem
Shor’s algorithm is used for prime factorisation. Quantum Mapping class has the properties of state and amplitude.
import math
import random
class QuantumMapping:
def __init__(self, state, amplitude):
self.state = state
self.amplitude = amplitude
Quantum State has properties amplitude, register, and entangled list. The entangle method of Quantum State class takes parameters from State and amplitude. The method sets the entangled to quantum state initialised with from State.
class QuantumState:
def __init__(self, amplitude, register):
self.amplitude = amplitude
self.register = register
self.entangled = {}
def SetEntangled(self, fromState, amplitude):
register = fromState.register
entanglement = QuantumMapping(fromState, amplitude)
try:
self.entangled[register].append(entanglement)
except KeyError:
self.entangled[register] = [entanglement]
The entangles method of Quantum State class takes register as the parameter and returns the length of the entangled states.
def GetEntangles(self, register = None):
entangles = 0
if register is None:
for states in self.entangled.values():
entangles += len(states)
else:
entangles = len(self.entangled[register])
return entangles
The Quantum Register class has numBits, numStates, entangled list and states array. SetPropagate of the Quantum Register class takes fromRegister as the parameter and sets the propagate on the register.
class QuantumRegister:
def __init__(self, numBits):
self.numBits = numBits
self.numStates = 1 << numBits
self.entangled = []
self.states = [QuantumState(complex(0.0), self) for x in range(self.numStates)]
self.states[0].amplitude = complex(1.0)
def SetPropagate(self, fromRegister = None):
if fromRegister is not None:
for state in self.states:
amplitude = complex(0.0)
try:
entangles = state.entangled[fromRegister]
for entangle in entangles:
amplitude += entangle.state.amplitude * entangle.amplitude
state.amplitude = amplitude
except KeyError:
state.amplitude = amplitude
for register in self.entangled:
if register is fromRegister:
continue
register.propagate(self)
SetMap method of the Quantum Register class takes toRegister, mapping and propagate as the parameters. This method sets the normalized tensorX and Y lists.
def SetMap(self, toRegister, mapping, propagate = True):
self.entangled.append(toRegister)
toRegister.entangled.append(self)
mapTensorX = {}
mapTensorY = {}
for x in range(self.numStates):
mapTensorX[x] = {}
codomain = mapping(x)
for element in codomain:
y = element.state
mapTensorX[x][y] = element
try:
mapTensorY[y][x] = element
except KeyError:
mapTensorY[y] = { x: element }
def SetNormalize(tensor, p = False):
lSqrt = math.sqrt
for vectors in tensor.values():
sumProb = 0.0
for element in vectors.values():
amplitude = element.amplitude
sumProb += (amplitude * amplitude.conjugate()).real
normalized = lSqrt(sumProb)
for element in vectors.values():
element.amplitude = element.amplitude / normalized
SetNormalize(mapTensorX)
SetNormalize(mapTensorY, True)
for x, yStates in mapTensorX.items():
for y, element in yStates.items():
amplitude = element.amplitude
toState = toRegister.states[y]
fromState = self.states[x]
toState.entangle(fromState, amplitude)
fromState.entangle(toState, amplitude.conjugate())
if propagate:
toRegister.propagate(self)
GetMeasure method of the Quantum Register class returns the final X state.
def GetMeasure(self):
measure = random.random()
sumProb = 0.0
finalXval = None
finalState = None
for x, state in enumerate(self.states):
amplitude = state.amplitude
sumProb += (amplitude * amplitude.conjugate()).real
if sumProb > measure:
finalState = state
finalXval = x
break
if finalState is not None:
for state in self.states:
state.amplitude = complex(0.0)
finalState.amplitude = complex(1.0)
self.propagate()
return finalXval
GetEntangles method of the Quantum Register class takes the register as the parameter and returns the entangled state value.
def GetEntangles(self, register = None):
entanglevals = 0
for state in self.states:
entanglevals += state.entangles(None)
return entanglevals
GetAmplitudes method of the Quantum Register class returns the amplitudes array based on the quantum states.
def GetAmplitudes(self):
amplitudesarr = []
for state in self.states:
amplitudesarr.append(state.amplitude)
return amplitudesarr
The list of entangles are printed out and the values of the amplitudes of the register are printed.
def ListEntangles(register):
print("Entangles: " + str(register.entangles()))
def ListAmplitudes(register):
amplitudes = register.amplitudes()
for x, amplitude in enumerate(amplitudes):
print('State #' + str(x) + '\'s Amplitude value: ' + str(amplitude))
ApplyHadamard method takes lambda x and Quantum bit as the parameters. The codomain array is returned after appending the quantum mapping of the Quantum bits.
def ApplyHadamard(x, Q):
codomainarr = []
for y in range(Q):
amplitude = complex(pow(-1.0, GetBitCount(x & y) & 1))
codomainarr.append(QuantumMapping(y, amplitude))
return codomainarr
The GetQModExp method takes parameters aval, exponent expval, and the modval operator value. The state is calculated using the method GetModExp. The quantum mapping of the state and the amplitude is returned by the method
def GetQModExp(aval, expval, modval):
state = GetModExp(aval, expval, modval)
amplitude = complex(1.0)
return [QuantumMapping(state, amplitude)]
ApplyQft method takes parameters x and Quantum bit. The codomainarr is returned after appending the quantum mapping of the quantum bits.
def ApplyQft(x, Q):
fQ = float(Q)
k = -2.0 * math.pi
codomainarr = []
for y in range(Q):
theta = (k * float((x * y) % Q)) / fQ
amplitude = complex(math.cos(theta), math.sin(theta))
codomainarr.append(QuantumMapping(y, amplitude))
return codomainarr
The GetPeriod method takes parameters a and N. The period r for the function is returned from this method.
def GetPeriod(a, N):
nNumBits = N.bit_length()
inputNumBits = (2 * nNumBits) - 1
inputNumBits += 1 if ((1 << inputNumBits) < (N * N)) else 0
Q = 1 << inputNumBits
print("Finding the period...")
print("Q = " + str(Q) + "\ta = " + str(a))
inputRegister = QuantumRegister(inputNumBits)
hmdInputRegister = QuantumRegister(inputNumBits)
qftInputRegister = QuantumRegister(inputNumBits)
outputRegister = QuantumRegister(inputNumBits)
print("Registers generated")
print("Performing Hadamard on input register")
inputRegister.map(hmdInputRegister, lambda x: hadamard(x, Q), False)
print("Hadamard complete")
print("Mapping input register to output register, where f(x) is a^x mod N")
hmdInputRegister.map(outputRegister, lambda x: GetQModExp(a, x, N), False)
print("Modular exponentiation complete")
print("Performing quantum Fourier transform on output register")
hmdInputRegister.map(qftInputRegister, lambda x: qft(x, Q), False)
inputRegister.propagate()
print("Quantum Fourier transform complete")
print("Performing a measurement on the output register")
y = outputRegister.measure()
print("Output register measured\ty = " + str(y))
print("Performing a measurement on the periodicity register")
x = qftInputRegister.measure()
print("QFT register measured\tx = " + str(x))
if x is None:
return None
print("Finding the period via continued fractions")
rperiod = cf(x, Q, N)
print("Candidate period\tr = " + str(rperiod))
return rperiod
GetBitCount method takes xval as a parameter. The sum of the bits in x is returned by this method.
def GetBitCount(xval):
sumBitvals = 0
while xval > 0:
sumBitvals += xval & 1
xval >>= 1
return sumBitvals
GetGcd method takes aval, bval as the parameters. The Greatest common denominator of aval and bval is returned by this method.
def GetGcd(aval, bval):
while bval != 0:
tA = aval % bval
aval = bval
bval = tA
return aval
GetExtendedGcd method takes a,b as the parameters. The extended Greatest common denominator of a and b is returned by this method.
def GetExtendedGCD(a, b):
fractionvals = []
while b != 0:
fractionvals.append(a // b)
tA = a % b
a = b
b = tA
return fractionvals
GetContinuedFraction method takes y, Q and N as the parameters. A continued fraction based on partial fractions which is derived from the extended Greatest common denominator is returned by this method.
def GetContinuedFraction(y, Q, N):
fractions = GetExtendedGCD(y, Q)
depth = 2
def partial(fractions, depth):
c = 0
r = 1
for i in reversed(range(depth)):
tR = fractions[i] * r + c
c = r
r = tR
return c
rcf = 0
for d in range(depth, len(fractions) + 1):
tR = partial(fractions, d)
if tR == rcf or tR >= N:
return rcf
rcf = tR
return rcf
The GetModExp method takes parameters aval, exponent expval, and the modval operator value. The power of a to the exponent which is operated by the Mod function using mod value is returned by this method.
def GetModExp(aval, expval, modval):
fxval = 1
while exp > 0:
if (exp & 1) == 1:
fxval = fxval * aval % modval
aval = (aval * aval) % modval
expval = expval >> 1
return fxval
RandomPick method takes input as N and returns the random value less than N.
def RandomPick(Nval):
aval = math.floor((random.random() * (Nval - 1)) + 0.5)
return aval
GetCandidates method takes a, r, N and neighborhood as the parameters. The candidates which have the period R are returned by this method.
def GetCandidates(a, r, N, neighborhood):
if r is None:
return None
for k in range(1, neighborhood + 2):
tR = k * r
if GetModExp(a, a, N) == GetModExp(a, a + tR, N):
return tR
for tR in range(r - neighborhood, r):
if GetModExp(a, a, N) == GetModExp(a, a + tR, N):
return tR
for tR in range(r + 1, r + neighborhood + 1):
if GetModExp(a, a, N) == GetModExp(a, a + tR, N):
return tR
return None
ExecuteShors method takes N, attempts, neighborhood, and numPeriods as parameters. This method executes the Shor’s algorithm to find the prime factors of a given Number N.
def ExecuteShors(N, attempts = 1, neighborhood = 0.0, numPeriods = 1):
periods = []
neighborhood = math.floor(N * neighborhood) + 1
print("N = " + str(N))
print("Neighborhood = " + str(neighborhood))
print("Number of periods = " + str(numPeriods))
for attempt in range(attempts):
print("\nAttempt #" + str(attempt))
a = pick(N)
while a < 2:
a = pick(N)
d = GetGcd(a, N)
if d > 1:
print("Found factors classically, re-attempt")
continue
r = findPeriod(a, N)
print("Checking candidate period, nearby values, and multiples")
r = GetCandidates(a, r, N, neighborhood)
if r is None:
print("Period was not found, re-attempt")
continue
if (r % 2) > 0:
print("Period was odd, re-attempt")
continue
d = GetModExp(a, (r // 2), N)
if r == 0 or d == (N - 1):
print("Period was trivial, re-attempt")
continue
print("Period found\tr = " + str(r))
periods.append(r)
if(len(periods) < numPeriods):
continue
print("\nFinding least common multiple of all periods")
r = 1
for period in periods:
d = GetGcd(period, r)
r = (r * period) // d
b = GetModExp(a, (r // 2), N)
f1 = GetGcd(N, b + 1)
f2 = GetGcd(N, b - 1)
return [f1, f2]
return None
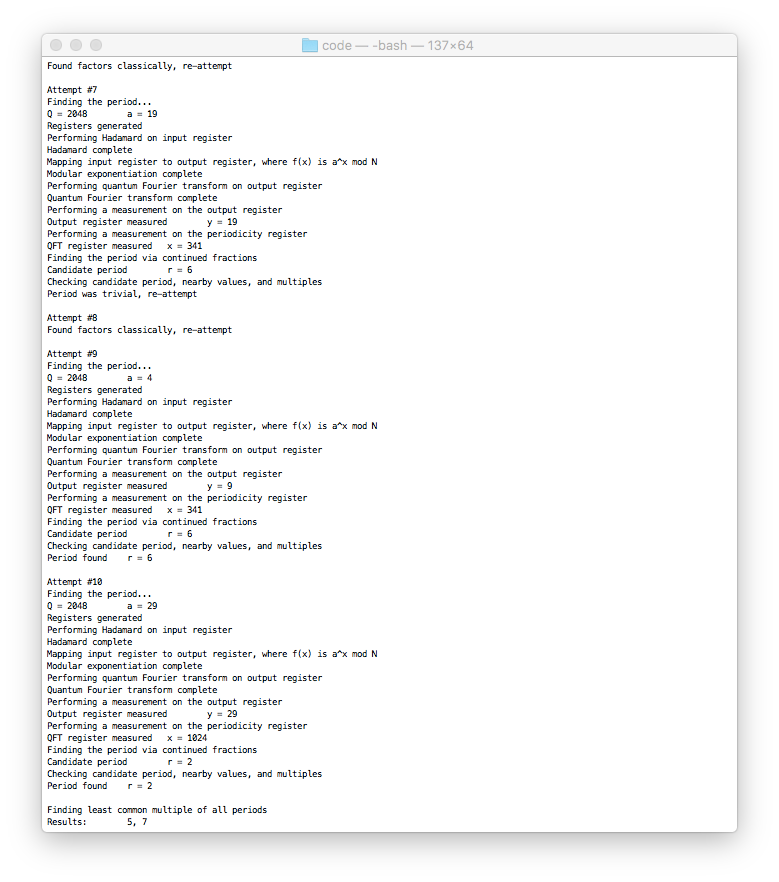
Results are obtained from the Shor’s algorithm and printed out.
results_algo = ExecuteShors(35, 20, 0.01, 2)
print(“Results from the algorithm:\t" + str(results_algo[0]) + ", " + str(results_algo[1]))
Instructions for Running the Code
#running the Shor’s Algorithm python code
python Shors.py
Output:
bhagvanarch
Guest Blogger


