June 6, 2019 Grover’s Algorithm in Quantum Computing

An algorithm must be seen to be believed.

Donald Knuth

This article will introduce Grover’s algorithm in the Quantum Algorithms series. The reader will learn how to implement Grover’s algorithm by using amplitude amplification, and how to analyze the performance of the algorithm.

The concept of the algorithm was initially not well defined in 1928.  Algorithms were performed using paper and pencil. For example, multiplication and division algorithms were long and used for huge numbers. In classical computing, the bit is the basic unit of information. The information can be broken down into patterns of 00s and 11s. They can be altered using binary operations.

Quantum computers are based on quantum bits. A quantum bit can have state 0 or 1 and it can be simultaneously in 0 and 1. The state of a quantum bit is represented in a vector form. It can be represented as |0> in Dirac notation. |0> and |1> are column vectors.  Let say 0.3|0>+ 0.1|1> state is a superposition of |0> and |1> . This means it is a linear combination of two states |0> and |1>. Amplitude is the coefficient of a state which is in superposition. For example, 0.5 |0> + 0.7 |1> superposition state, amplitude for |0> is 0.5 and |1> is 0.7.

Computational complexity is measured based on execution time and space used for the scenario.  The number of basic operations is the measure for the execution time. In quantum computing, quantum circuit model consists of basic quantum gates which are operations. Quantum gates operate on quantum bits.

Grover’s algorithm is of order  O(√ n) evaluations in execution time. The algorithm gives a reasonable speed advantage for unstructured search. For example, searching for a phone number in a phone book in a normal search takes n/2 steps. Grover’s algorithm takes √ n steps.

The code below shows a Grover’s algorithm implementation. In this implementation, we look at the search based on Grover’s algorithm.

Prerequisites:

1. You need to set up Python3.5 to run the code samples below. You can download from this link.

Problem

The Grover’s search algorithm searches the target value from a set by calculating the mean amplitude and the Grover’s amplitude. The plot of the graph is calculated from the amplitudes derived from the Grover’s algorithm. The plot shows the target value with the highest amplitude.

import matplotlib.pyplot as plt
import numpy as np
import string
import hashlib
from math import sqrt, pi
from collections import OrderedDict
from statistics import mean
def ShowGraph(amplitude_value, n):
    y_position = np.arange(n)
    plt.bar(y_position, amplitude_value.values(), align='center', color='g')
    plt.xticks(y_position, amplitude_value.keys())
    plt.ylabel('Amplitude Value')
    plt.title('Grovers Algorithm')
    plt.show()

GetOracle method takes the xvalue and returns the hex digest of the x value. This method is referred to as the Oracle function.

def GetOracle(xvalue):
    return hashlib.sha256(bytes(xvalue, 'utf-8')).hexdigest()

Execute Grover’s algorithm takes input target, objects, nvalue and rounds.  The amplitude is retrieved based on the 1/ square root of the nvalue.

def ExecuteGrover(target, objects, nvalue, rounds):
    y_pos = np.arange(nvalue)
    amplitude = OrderedDict.fromkeys(objects, 1/sqrt(nvalue))
    for i in range(0, rounds, 2):
        for k, v in amplitude.items():
            if GetOracle(k) == target:
                amplitude[k] = v * -1
        average = mean(amplitude.values())
        for k, v in amplitude.items():
            if GetOracle(k) == target:
                amplitude[k] = (2 * average) + abs(v)
                continue
            amplitude[k] = v-(2*(v-average))
    return amplitude

The target of the algorithm is to search for ‘3’ in the set of objects {‘4’, ‘5’, ‘3’, ‘7’,’9′,’11’,’97’}.  The amplitude is searched from the dictionary based on the value 1/ square root of the length of the set (7).

target_algorithm = '3'
objects_grover = ('4', '5', '3', '7','9','11','97')
number = len(objects_grover)
amplitude_grover = OrderedDict.fromkeys(objects_grover, 1/sqrt(number))

The mean of the amplitudes is calculated and printed.  The Grover amplitude is calculated based on the average amplitude and the Grover’s operator. The Grover’s operator is  defined as (2|xi> <xi| – average_amplitude) * Oracle function

amplitude_grover[target_algorithm] = amplitude_grover[target_algorithm] * -1
print(amplitude_grover)
average_grover = mean(amplitude_grover.values())
print("Mean is {}".format(average_grover))
for k, v in amplitude_grover.items():
    if k == target_algorithm:
        amplitude_grover[k] = (2 * average_grover) + abs(v)
        continue
    amplitude_grover[k] = v-(2*(v-average_grover))
print(amplitude_grover)

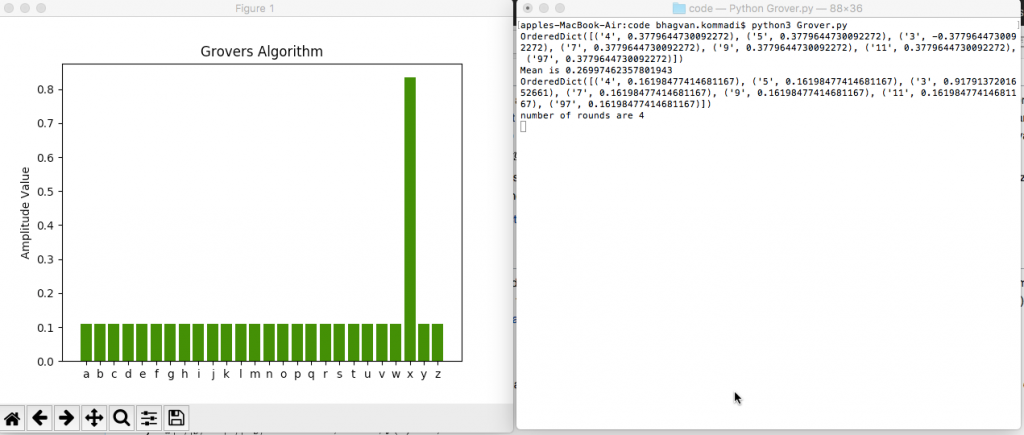
The amplitudes are plotted after running the Grover’s algorithm. The target value ‘3’ has the highest amplitude 0.9.

needle_value = "2d711642b726b04401627ca9fbac32f5c8530fb1903cc4db02258717921a4881"
haystack_value = string.ascii_lowercase
num = len(haystack_value)
num_rounds = int((pi / 4) * sqrt(num))
print("number of rounds are {}".format(num_rounds))
ShowGraph(ExecuteGrover(needle_value, haystack_value, num, num_rounds), num)

Instructions for Running the Code

#running the Grover’s Algorithm python code
python Grover.py

Output