April 2, 2017 Final Results Of Marathon Match 93

The final standings of Marathon Match 93 were published on March 28. You can check the source code of all participants by clicking on “Submission History” column of a particular competitor. The leaderboard changes are rather minor, compared to some of the data mining competitions from the past.

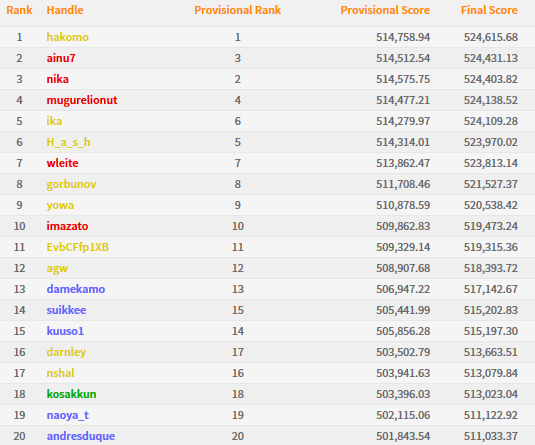
Congratulations to hakomo and the top-5, who gained 524,000+ final score!

Analysis Of Solutions

It looks like all the solutions from the Top-10 use the Simulated Annealing (SA) technique briefly mentioned in my previous TCO blog article. The main idea turned out to be the reduction of the task to the well-studied Travelling Salesman Problem (TSP).

What Is TSP

In mathematical terms, the TSP asks to find the shortest cycle that visits all the vertices of a graph. A common sample application of this problem is to help the salesman to minimize the cost of visiting all the cities from a set. On practice, the mathematical description has a bigger use, because it obviously does not have the constraint of being applicable to salesmen business only.
The exact algorithms to this task are of exponential time complexity. This implies that even if implemented properly and launched on supercomputers, it is unlikely they will solve the task of this match in 10 seconds.
Some good approximate algorithms, also called heuristics, exist. They are able to produce results that are not necessary the best solutions to the task, in a feasible amount of time. The difference in quality between optimal solutions and heuristic solutions for this match, by my estimates, was under 2%.

The Reduction

There were a few hooks in this match task that did not allow to apply the TSP solutions directly. Let us list them:

• Stitch on the front side must represent a diagonal of a single cell. This effectively means that |xi – xi+1| = 1 and |yi – yi+1| = 1 for all even i, 0-based.
• We may have up to 4 vertices that are placed in the same Euclidean point. The task forbids us to place two consecutive vertices that represent the same point.
• We have stitches of different colors, each color needs to be solved separately.
• We need a path, but the classical TSP task is about the tour, or cycle.

In order to deal with the first restriction, it is enough to generate some proper solution in the beginning of the algorithm, and just keep the solution valid later. Valid solutions are retrieved by forbidding the cut-and-replace of any front diagonal in the process of improving the solution, i.e. the (i, i + 1) edge, where i is even, must be kept. The only allowed operation on the front stitches, or edges, is to swap the order of their endpoints.
As for the second restriction, we also follow the solution is always valid invariant. Indeed, we ignore a solution that is better than the current, if it breaks the rule of no two consecutive points that are the same.
The third issue is the simplest one. We can either split the time between all the colors, and solve each color independently, or solve them with a pseudo-parallel, Round-Robin schedule.
The fourth problem may be solved by introducing pseudo-vertices in the front and in the end of the path that have 0 distance to all the other vertices. Another option is to add several if-statements into the code, which turned out to be a worse decision.
Once these problems are resolved, we may try to apply some generic TSP technique.

Constructing The Initial Solution

The Simulated Annealing assumes we have some initial solution, or state, to start with.
A random solution, as the initial state, turned out to be the best option for me in this match. To construct it, we need to store a 2D array of bit flags, each item of the array representing 2 diagonals of a cell of the given board. Let us call it diagonal. If the main diagonal of a cell (i, j) is already used, we set diagonal[i][j] |= 1. If the secondary diagonal of that same cell is used, we set diagonal[i][j] |= 3.
Now, let us construct the initial solution in an iterative manner. On each step we can add a random diagonal of a random cell, in case it is not already added. Continuing that way, eventually we will construct a valid solution. There is a little caveat here, however. We must be careful with the back side, where no 2 consecutive vertices of the path can represent the same plane point. To accomplish that, we just swap the direction of the last added diagonal, in case this rule is not fulfilled.
A greedy state could also be used as initial, but my tests have shown that is is worse on practice. Probably this is due to an additional hardness of escape from the local minimum associated with the greedy.

The Data Structure

The simplest data structure for storing an ordered list of vertices of the solution is probably a plain old array. hakomo stored indices of the vertices on the current-best path in this array. I stored the coordinates of vertices in order they appear on the path, in an attempt to avoid an extra array dereferencing and thus optimizing the performance. Howeverut this complicated the solution and turned out to reduce the amount of possible good algorithmic optimizations.
Another approach is to store an ID of a front diagonal, as well as its orientation. nika went this way.

The Main Transition Part

Once we have chosen the SA as the technique of choice for this task, the first thing to do is to define state transition functions.
The usual transitions for the TSP are the so-called 2-opt swaps. They essentially break two edges of the current solution and re-connect the remaining parts in a new fashion so that the result is still a valid single-cycle around the graph (or a path, if you prefer not to introduce the two pseudo-vertices).

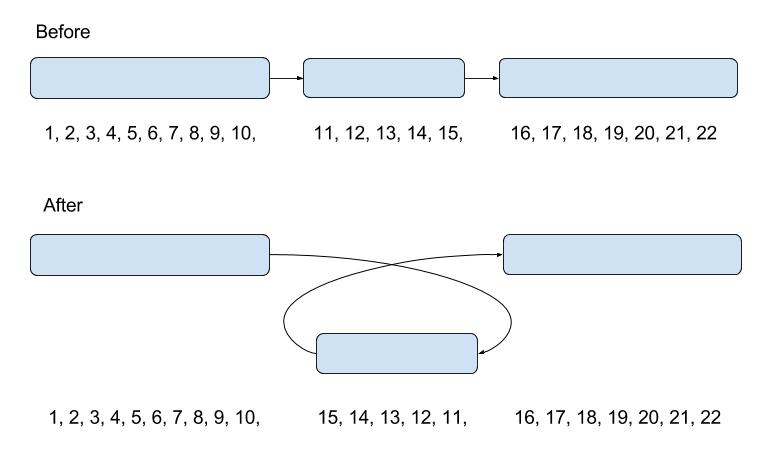
Once you have an array of vertices, in their order, you can do the 2-opt that involves breaking of edges (xi, yi)↔(xi+1, yi+1) and (xj, yj)↔(xj+1, yj+1), by reversing the order of vertices with indices in range [i+1..j]. This effectively breaks the links i↔(i+1) and j↔(j+1), and replaces them with new links, i↔j and (i+1)↔(j+1).

The Main Trick

The main trick becomes obvious once you notice that it is hardly probable that two front diagonals that are too far apart, will be connected in an optimal solution. This is very true when a diagonal is in the middle of a block of cells of the same color. On the other side, it is most probably useless to remove two back stitches of unity length.
This leads to a simple, but powerful heuristic: the first edge i↔(i+1) to remove is of length greater than 1, and the second edge to remove resides somewhere near the vertex (i+1).
hakomo decided that it is enough to try just diagonals containing vertices that are Euclidean neighbors of the vertex (i + 1), as the second diagonal to remove. He determined amount of Euclidean neighbors to consider empirically to be 29 for small size boards, and 17 for larger boards. Note that the second diagonal to remove, unlike the first, may be of unity length.
mugurelionut followed a somewhat similar, but more complex way of determining the neighbor diagonals. He assumed that edges that are contained in the Minimum Spanning Tree (MST) of the input graph, are more probable to be in the result path, and thus deserve a special importance. He introduced an alpha-neighbour distance between two diagonals, calculated as an Euclidean distance between the diagonal endpoints minus length of the longest edge in the MST that is in turn on the path between the two diagonals. I guess he should have added some coefficient to the MST-part of the formula. Otherwise, the alpha-neighbor distance might be biased towards edges that are in the MST, even if they are of little use to the optimal TSP path.

The Dynamic Programming

A minor, but important score increase can be obtained by introducing an unlikely, long-running, but powerful transition function called optimization of the path.
I limited it to just changing directions of diagonals, without affecting their order, so that the result is better than the current solution. This can be done by a forward DP. The state is (number of processed diagonals, did we change the direction of the last diagonal), and the question of the DP is the shortest length of the TSP path, after we have modified it by the mentioned change of direction of the diagonals.
hakomo went further, by allowing the DP to swap two consecutive diagonals.

The Details

The first thing to note is that it is useless to rely on the given scoring formula as the delta for SA. It is preferable to use the plain total length of the path instead, as it is linear, and there are no negative values for it, opposed to the score function of the problem, where the function shape is cubic, and the negative values are possible.
Do not use the sqrt function all the time you need a square root. It is slow, very slow compared to simple arithmetical operations, like addition or multiplication. Storing a precalculated table of square roots of numbers up to 2002 was enough. Some competitors stored a table of distances between vertices. Depending on other data structures used in the solution, one or the other might be better. The sqrt-table is smaller and thus more likely to fit into a lower cache layer. The distance table, however, has an advantage of being all-done, and no extra arithmetics is needed in order to get the distance between two vertices.
Another detail worth mentioning it again is the separate cost calculation function for the most probable transitions. Namely, when you prepare a 2-opt swap, you can easily calculate the delta of the score it will give you. Try to look at the picture of this operation and derive the formula if you have not done so yet.

Final notes

You can view each competitor’s source code by visiting here, clicking on the last column of a participant’s row, and clicking on the submission number.
The next match will be the TCO17 Qualification 1, starting on April 12. Have a good rest and see you there!