June 13, 2019 2019 TCO Algorithm Round 2B Editorial
MedianFaking
Statement
You have ? sets of ? measurements each. You have to change result of some measurements in such a way that median of the whole set of measurements becomes exactly ????. Among all such changes you have to find the one having minimum possible amount of changed sets ? and among such changes you have to find the one having minimum total amount of changed measurements ?. Note that for even-sized arrays median is the smaller of two middle elements.
Solution
Let ?=?⋅? to be the total number of measurements. To begin with, calculate for each set ???? which is amount of measurements within the set having result lower than ???? and ???? which is the number of measurements having result greater than ????. Let total_les and total_gre be the sum of ???? and ???? over all ?correspondingly. To make ???? the median we should change some elements counted in either total_les or total_gre into ????. First of all, we should decide on how much elements we should change. For ???? to be median it must hold that:
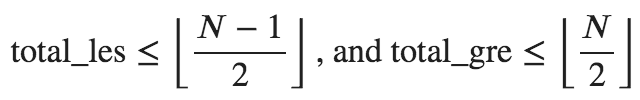
Thus we may define dif_le and gif_ge being equal to the minimum possible number of elements counted in total_les and total_gre respectively which must be changed to ???? in order to make ???? the median. Note that since total_les+total_gre≤? eitler dif_le or dif_ge will be equal to 0. Obviously, in optimal solution there’s no need to change anything from the set having dif=0 into goal as it will only increase total number of changed elements. Now that we know which type of measurements we should change and how many of them should be changed, we simply sort all sets via ???? or ???? (whichever of dif_le or dif_geis non-zero) in descending order and keep taking them until we fulfil corresponding dif number. Please look into the code for further understanding.
Code:
vector <int> minimize(int F, int M, vector <int> data, int goal) {
int N = F * M;
vector<int> les(F), gre(F);
for(int i = 0; i < F; i++) {
int le = 0, ge = 0;
for(int j = 0; j < M; j++) {
le += data[i * M + j] < goal;
ge += data[i * M + j] > goal;
}
les[i] = le;
gre[i] = ge;
}
int total_les = accumulate(begin(les), end(les), 0);
int total_gre = accumulate(begin(gre), end(gre), 0);
int dif_le = max(0, total_les - (N - 1) / 2);
int dif_ge = max(0, total_gre - N / 2);
if(dif_le < dif_ge) {
swap(dif_le, dif_ge);
swap(total_les, total_gre);
swap(les, gre);
}
sort(begin(les), end(les), greater<int>());
int cnt = 0, ans = dif_le;
for(auto it: les) {
if(dif_le <= 0) {
break;
}
cnt++;
dif_le -= it;
}
return {cnt, ans};
}
DivisorSequences
Statement
You’re given integer ?. You have to find the length of longest possible sequence ?1,…,?? such that:
- ?1+⋯+??=?,
- ??<??+1 for all valid ?,
- ?? divides ??+1 for all valid ?.
Solution
Let ?(?) be the maximum length of such sequence that doesn’t start with 1. Then the answer would be equal to the maximum of ?(?) and ?(?−1)+1. But for this function it is easy to come up with recurrent formula:
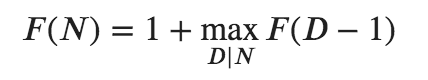
Here ? passes through all divisors of ? except for ? itself. Explanation here as follows: since all ?? are divisible by ?1 we may say that ? is divisible by ?1 as well. If we try all possible ?1 among divisors of ?, we will see that after we used ?1 we have to split the number ?−?1 into similar sequence but having all elements divisible by ?1. The length of such sequence would be equal to:
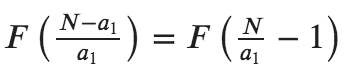
Thus if we consider all values of ?=??1 except for ?=? which goes from ?1=1, we’ll obtain the formula mentioned above.
It is pretty hard to make proper estimation of time complexity for solutions using this formula as they turn out to be extremely fast even if you don’t even store already computed values and simply compute them from scratch. For solution with memorization of already computed values estimation might be an ?(?2/3) as number ? generally has at most ?‾‾√3 distinct divisors and you look on each pair {?|?} of nested divisors at most once. But actual running time is greatly less.
Code:
const int maxn = 4e5;
int prec[maxn];
unordered_map<int, int> gg;
int get_ans(int n) {
if(n <= 1) {
return 0;
} else if((n < maxn ? prec[n] : gg[n])) {
return (n < maxn ? prec[n] : gg[n]);
} else {
int res = 1;
for(int i = 2; i * i <= n; i++) {
if(n % i == 0) {
res = max({res, 1 + get_ans(n / i - 1), 1 + get_ans(i - 1)});
}
}
return (n < maxn ? prec[n] : gg[n]) = res;
}
}
int longest(int N) {
for(int i = 1; i < maxn; i++) {
get_ans(i);
}
return max(get_ans(N), 1 + get_ans(N - 1));
}
DivisorSequences
Statement
Two players are playing a game. Each choose a positive integer (let them be ? and ?), after that:
- If ?=?, then the game is a draw and there’s no payment,
- If |?−?|≤? then player with bigger number gets ? dollars from the other one,
- If |?−?|>? then player with smaller number gets ?≥? dollars from the other one.
Strategy of a player may be described by the sequence ?1,?2,… of probabilities to choose each number.
Consider the lexicographically largest strategy which maintains Nash equilibrium. Given number ?, you have to output ??.
Solution
Let the strategies of both players be ?1,?2,… and assume that they’re in Nash equilibrium. Expected profit may be written as:
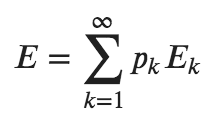
Where ?? is expected value of profit after player chose ?. It can be expressed with the following formula:
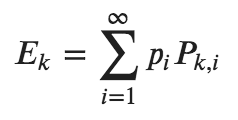
Where ??,? is profit we get if we play ? and opponent plays ?. Now note that if ??>?? and ??≠0 then we may get better expected value if we turn ?? to 0 and raise ?? by the initial value of ??. Thus if ??≠0 and ??≠0 then ??=??. Also say if ??=0 and ??≠0 then ??≥??, so expected profit for values ? with ??≠0 will all have the same ?? which is at least as large as any ?? for ??=0.
It’s still not enough to find the strategy uniquely. Next thing to note now is that ??≤?1 for ?>2?+1 because ??,?≤?1,? for all ? and all ?>2?+1. Thus if we consider arbitrary strategy ?1,?2,… we will get a strategy with at least same expected value of profit if we turn all ?? to 0 for ?>2?+1 and increase ?1instead. New strategy would also be lexicographically larger then initial one.
In this way we’re only interested in strategies with ??=0 for ?>2?+1 and ??=?? for ?,?≤2?+1. We may find it uniquely if we solve the system of 2?+1 equations, first one being ![]() and all the others being ?1=?? for ? from 2 to 2?+1.
and all the others being ?1=?? for ? from 2 to 2?+1.
Code:
public double getProbability(int D, int N, int F, int query) {
if (query > 2*D+1) return 0.;
double[][] P = new double[2*D+1][2*D+1];
for (int a=0; a<=2*D; ++a) for (int b=0; b<=2*D; ++b) {
if (a == b) P[a][b] = 0.;
if (1 <= a-b && a-b <= D) P[a][b] = N;
if (D < a-b) P[a][b] = -F;
if (1 <= b-a && b-a <= D) P[a][b] = -N;
if (D < b-a) P[a][b] = F;
}
double[][] E = new double[2*D+1][2*D+2];
for (int d=0; d<=2*D+1; ++d) E[0][d] = 1.;
for (int r=1; r<=2*D; ++r) for (int d=0; d<=2*D; ++d) E[r][d] = P[r][d] - P[0][d];
// gauss
for (int r=0; r<=2*D; ++r) {
int biggest = r;
for (int r2=r; r2<=2*D; ++r2) if (Math.abs(E[r2][r]) > Math.abs(E[biggest][r])) biggest = r2;
for (int c=0; c<=2*D+1; ++c) { double t = E[r][c]; E[r][c] = E[biggest][c]; E[biggest][c] = t; } // swap rows
for (int r2=r+1; r2<=2*D; ++r2) {
double mul = E[r2][r] / E[r][r];
for (int c=r; c<=2*D+1; ++c) E[r2][c] -= mul*E[r][c];
}
}
double[] ans = new double[2*D+1];
for (int r=2*D; r>=0; --r) {
double rhs = E[r][2*D+1];
for (int c=r+1; c<=2*D; ++c) rhs -= E[r][c] * ans[c];
ans[r] = rhs / E[r][r];
}
return ans[query-1];
}
Guest Blogger
