April 24, 2019 2019 Insomnia Editorials
GreaterThanAll
Statement
Consider sequence \(A = {a_1, \dots, a_n}\). Define \(Peak_Set = {a[i] : a[i] > a[j] \text{ for all } j < i}\).
For given \(N, K \leq 10^6\) calculate number of sequences \(X\) of length \(N\) with \(Peak_set(X) = {1,2,\dots,K}\).
Solution
Basically you should calculate the following sum:
\(\sum\limits_{k_1+\dots+k_K = N-K} 1^{k_1} 2^{k_2} \dots K^{k_K} = [x^{N-K}] \left(\frac{1}{1-x} \frac{1}{1-2x} \dots \frac{1}{1-Kx}\right)\)Here \([x^k]P(x)\) stands for coefficient near \(x^k\) of expansion of \(P(x)\). Now we should note that rationaly function can be rewrited as:
\(\frac{1}{(1-x)(1-2x)\dots(1-Kx)} = \frac{A_1}{1-x} + \frac{A_2}{1-2x} + \dots + \frac{A_K}{1-Kx}\)Multiplying it with \((1-2x)\dots(1-Kx)\) on both sides, we obtain:
\(1=\sum\limits_{k=1}^K A_k \prod\limits_{j \neq k}(1-jx)\)This allows us to get \(A_k\) explicitly by substituting \(x=k^{-1}\):
\(A_k = \frac{1}{\prod\limits_{j \neq k}(1-\frac{j}{k})}=\frac{k^{K-1}}{\prod\limits_{j\neq k}(k-j)}=\frac{(-1)^{K-k}k^{K-1}}{(k-1)!(K-k)!}\)Which allows us to write the final answer:
\(Ans = \sum\limits_{k=1}^K A_k k^{N-K}=(-1)^K\sum\limits_{k=1}^K \frac{(-1)^{k}k^{N-1}}{(k-1)!(K-k)!}\)Code:
const int64_t mod = 1e9 + 7;
int bpow(int64_t x, int64_t n) {
return n ? n % 2 ? x * bpow(x, n - 1) % mod : bpow(x * x % mod, n / 2) : 1;
}
int inv(int64_t x) {
return bpow(x, mod - 2);
}
int count(int N, int K) {
int ans = 0;
int fact[K];
fact[0] = 1;
for(int k = 1; k < K; k++) {
fact[k] = 1LL * fact[k - 1] * k % mod;
}
for(int k = 1; k <= K; k++) {
int t = 1LL * bpow(k, N - 1) * inv(fact[k - 1]) % mod * inv(fact[K - k]) % mod;
ans += (k % 2 ? mod - t : t);
ans %= mod;
}
return (K % 2 ? mod - ans : ans) % mod;
}
SubstringReversal2
Statement
You’re given string \(S\) of length \(N \leq 200\). Consider subsequence \(p_1,\dots,p_{2k}\) of \(1,2,\dots,N\).
Now construct new string \(S’\) as follows: reverse substring from \(p_{2i-1}\) to \(p_{2i}\) for all \(i\) from \(1\) to \(k\).
Consider all possible \(S’\), you have to find \(k\)-th lexicographically largest such string.
Solution
To solve this problem you should try to append characters to the string one by one and check how many many strings it’s possible to collect with given prefix, which may be done via quadratic DP. It produces kind of straight forward solution, but it has lots of technicalities, thus you’re recommended to look in the code to learn details. Total complexity is going to be \(O(\Sigma n^3)\) where \(\Sigma\) is the size of alphabet.
Code:
private static final int N = 205;
private char[] t;
private char[] s;
private long[] dp = new long[N];
private long n;
private boolean[][] dp1 = new boolean[N][N];
private boolean match(int i,int j){
if(t[j - 1] == '$') return true;
return s[i - 1] == t[j - 1];
}
private boolean check(int i,int j){
return (match(i, j) && match(j, i));
}
private long f(long k){ // O(n^2)
Arrays.fill(dp, 0);
dp[0] = 1;
for(int i = 1; i <= n; ++i){
dp1[i][i] = match(i, i);
if(i < n && check(i, i + 1))
dp1[i][i + 1] = true;
else
dp1[i][i + 1] = false;
}
for(int l = 2; l <= n; ++l){
for(int i = 1; i <= n - l; ++i){
dp1[i][i + l] = (dp1[i + 1][i + l - 1] && check(i, i + l));
}
}
for(int i = 0; i <= n - 1; ++i){
if(match(i + 1, i + 1)) dp[i + 1] += dp[i];
if(dp[i + 1] > k) dp[i + 1] = k + 1;
for(int j = i + 2; j <= n; j++){
if(dp1[i + 1][j]) dp[j] += dp[i];
if(dp[j] > k) dp[j] = k + 1;
}
}
return dp[(int)n];
}
public String solve(String ss, long k){
s = ss.toCharArray();
n = s.length;
t = new char[(int)n];
Arrays.fill(t, '$');
for(int i = 0; i <= n - 1; ++i){ // O(N*26)
for(int j = 0; j <= 25; ++j){
t[i] = (char)('a' + j);
long val = f(k);
if(val >= k) break;
else k -= val;
}
}
return new String(t);
}
BobTheBuilder
Statement
Consider \(N\) boxes with their costs given as \(A_0,\dots,A_{N-1}\). You may place \(i\)-th box into \(j\)-th one if \(A_j\) is divisible by \(A_i\).
You have to place boxes inside each other in a way that maximizes sum of costs of boxes which are not place in any other box.
Solution
Consider bipartite graph having \(N\) vertices in both parts. Vertex \(i\) from first part and vertex \(j\) from second part are connected if \(i\)-th box may be placed inside \(j\)-th one. Now we have one-to-one correspondence between placings of the boxes and matchings in this graph. Thus we have to find matching which maximizes sum of vertex costs from the first part of the graph. This is kind of well known problem and is solvable by Kuhn’s algorithm for finding maximum matching in bipartite graph after vertices are sorted by their costs.
Code:
const int maxn = 402;
vector<int> g[maxn];
int con_with[maxn];
void add_edge(int a, int b) {
g[a].push_back(b);
}
int used[maxn];
void prepare() {
memset(used, 0, sizeof(used));
}
bool try_kuhn(int v) {
if(!used[v]) {
used[v] = 1;
for(auto u: g[v]) {
if(con_with[u] == -1 || try_kuhn(con_with[u])) {
con_with[u] = v;
return true;
}
}
}
return false;
}
long long minimumCost(int N, vector <int> A) {
memset(con_with, -1, sizeof(con_with));
sort(begin(A), end(A));
for(int i = 0; i < N; i++) {
for(int j = i + 1; j < N; j++) {
if(A[j] % A[i] == 0) {
add_edge(i, j);
}
}
}
int64_t ans = 0;
for(int i = N - 1; i >= 0; i--) {
prepare();
ans += A[i] * !try_kuhn(i);
}
return ans;
}
CountingToOne
Statement
Consider a sequence \(f\) which satisfies:
\sum\lim_{d|n} f(d) \cdot f(n/d) = 1, \text{ for } n > 1\)
You have to calculate \(f(N) \pmod{10^9+7}\).
Solution
From this definition you may see that:
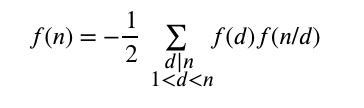
Which allows us to calculate \(f(n)\) directly if we know \(f(d)\) for \(d\) running through all divisors of \(n[latex].
Another useful observation is that [latex]f(n)\) defined in this way is multiplicative, that is if \(n=p_1^{k_1} \dots p_m^{k_m}\), then \(f(n) = f(p_1^{k_1}) \dots f(p_m^{k_m})\).
This allows us to calculate \(f(n)\) efficiently. To do this we should factorize \(n\) in \(O(\sqrt n)\) and then calculate \(f(p_i^{k_i})\) for all prime divisors of \(n\) in \(O(\log^2 n)\).
Code:
const int inv2 = inv(2);
unordered_map<long long, int> res;
int calculate_pr(long long n) {
if(n == 1) {
return 1;
} else if(res.count(n)) {
return res[n];
} else {
int64_t ans = 1;
for(long long i = 2; i * i <= n; i++) {
if(n % i == 0) {
int t = (mod * mod - 1LL * calculate(i) * calculate(n / i)) % mod;
ans += i * i == n ? t : 2 * t;
ans %= mod;
}
}
return res[n] = ans * inv2 % mod;
}
}
int calculate(long long n) {
int64_t res = 1;
for(int64_t i = 2; i * i <= n; i++) {
if(n % i == 0) {
int64_t t = 1;
while(n % i == 0) {
t *= i;
n /= i;
}
res *= calculate_pr(t);
res %= mod;
}
}
if(n > 1) {
res *= calculate_pr(n);
res %= mod;
}
return res;
}
StrangeColoring
Statement
You have to calculate number of ways to split \(N\) elements into at most \(M\) groups for \(M \leq 10^6\).
Number of ways to split \(N\) elements in exactly
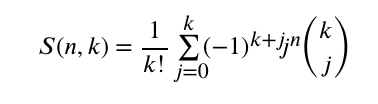
We basically have to calculate \(F(n,k) = S(n,1) + S(n,2) + \dots + S(n,k)\), it may be done as follows after we group summands:
Code:
int count(long long n, long long m) {
swap(m, n);
m = min(n, m);
fact[0] = 1;
for(int i = 1; i < maxn; i++) {
fact[i] = 1LL * fact[i - 1] * i % mod;
}
int d[m + 1];
d[0] = 1;
for(int i = 1; i <= m; i++) {
d[i] = (d[i - 1] + (i % 2 ? mod - inv(fact[i]) : inv(fact[i]))) % mod;
}
int64_t res = 0;
for(int i = 0; i <= m; i++) {
res += 1LL * bpow(i, n) * inv(fact[i]) % mod * d[m - i] % mod;
res %= mod;
}
return res;
}
Guest Blogger


