
|
Match Editorial |
Saturday, April 12, 2008
Match summary
This prime numbered SRM gathered together 1352 coders that were faced with a rather hard problem set. However, ACRush rushed
through the set achieving his new highest rating. Congratulations!
The match in division one started slowly, as the easy problem was not so easy to code. kia was the first one to submit the 250 and after his submit, solutions started to come in. Then, after about 15 minutes from
the beginning of the coding phase, we could saw the first submissions on the medium. From then, until the last minute of the coding phase,
solutions to the medium and the hard were coming in. After the coding phase
ACRush was on top, with Loner and
ahyangyi being close behind. Challenge phase was rather quiet, but unfortunately
ahyangyi's hard got challenged and bmerry
took his spot. wojtekt and gawry rounded
up the top five.
In division two, the whole match passed by rather smoothly, although there weren't too many submissions to the medium and hard problems (and out
of 128 hard submissions, only 21 were correct). After all, mrtempo won the division, with a
newcomer barney and royappa rounding up
the top three.
The Problems
BreakingTheCode

Used as: Division Two - Level One:
Value 250 Submission Rate 718 / 786 (91.35%) Success Rate 615 / 718 (85.65%) High Score brosmike for 245.21 points (3 mins 59 secs) Average Score 191.16 (for 615 correct submissions)
This problem was just a simple simulation of the algorithm described in the statement. If there are only letters in the message, we replace each letter with its assigned number. And if there are only digits, we take every two consecutive ones and replace them with a letter that's assigned the given code. This should be clear enough, but you can see the fastest submission by brosmike for reference.
SortingGame

Used as: Division Two - Level Two:
Used as: Division One - Level One:
Value 500 Submission Rate 145 / 786 (18.45%) Success Rate 92 / 145 (63.45%) High Score SlNPacifist for 467.77 points (7 mins 33 secs) Average Score 284.87 (for 92 correct submissions)
Value 250 Submission Rate 474 / 560 (84.64%) Success Rate 436 / 474 (91.98%) High Score kia for 247.29 points (2 mins 59 secs) Average Score 174.78 (for 436 correct submissions)
Low constraints guaranteed that there were no more than 8! = 40320 possible states. So, how can we find the shortest path from the initial state to a final one? By BFS, of course. We only need to map the states that can be represented by vectors, numbers or strings to their values, that are lengths of the respective shortest paths. It is easy to generate the permutations that we can achieve from the given one in one move. Please see the fastest and extremely clear implementation of the above by kia. This code shows, that in C++, the STL could solve the problem for us.
CollectingMarbles

Used as: Division Two - Level Three:
Value 1000 Submission Rate 127 / 786 (16.16%) Success Rate 21 / 127 (16.54%) High Score eagaeoppooaaa for 832.33 points (13 mins 19 secs) Average Score 634.81 (for 21 correct submissions)
This problem was rather standard. With at most 13 marbles we can represent the state as a set of marbles that we already have, the number of bags left, and the space left in the bag we are trying to fill now. So we start with an empty set, numberOfBags bags and bagCapacity space left in the bag we're filling. In each state we can either put to the current bag any marble we don't have yet or put the current bag aside and start to fill the next one. Representing sets as bit masks gives us approximately 213 * 20 * 10 = 1638400 possible states. That's ok to use memoization on them and with a simple recursion compute the answer. Sample Java implementation follows:
public class CollectingMarbles {
int[][][] dp;
int[] w;
int c;
public int recur (int mask, int left, int cur) {
if (left == 0) return 0;
if (dp[mask][left][cur] == -1) {
dp[mask][left][cur] = 0;
for (int i = 0; i < w.length; i++)
if ((mask & (1 << i)) == 0 && w[i] <= cur)
dp[mask][left][cur] = Math.max( dp[mask][left][cur],
1 + recur(mask | (1 << i), left, cur - w[i]));
dp[mask][left][cur] = Math.max( dp[mask][left][cur],
recur(mask, left - 1, c));
}
return dp[mask][left][cur];
}
public int mostMarbles (int[] mW, int bC, int nOB) {
w = mW;
c = bG;
dp = new int[1 << w.length][nOB + 1][c + 1];
Arrays.fill(dp, -1);
return recur(0, nOB, c);
}
}
SumOfPowers


Used as: Division One - Level Two:
Value 500 Submission Rate 158 / 560 (28.21%) Success Rate 98 / 158 (62.03%) High Score Loner for 447.83 points (9 mins 56 secs) Average Score 288.51 (for 98 correct submissions)
Well, this problem was an interesting one. The idea, with its simplicity and mathematical
background, caused many coders to search the internet for the formula. It could end with a
success, but not necessarily. Many coders, after reading all these formulas with Bernoulli
numbers were angry at the problem as they thought that you have to be a genius to come up with them.
Well, maybe you have to be, and maybe Bernoulli was. But what if he had Google? Maybe
he wouldn't even bother to invent all this stuff. Ok, so suppose that we don't have Google.
What do we have here? We are given the sum 1k + 2k + ... +
nk. Ok, let ai = 1k + ... + ik.
Everyone who finished high school knows that
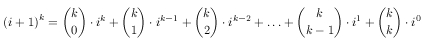 .
.Pascal showed us some day how we can effectively compute binomial coefficients, so let's suppose that we know their values and forget about them. So it looks like we have some number of recursively defined sequences. Now, the second thing that every top coder should know. The most obvious way to find the n-th term of a recursive sequence is to use a matrix multiplication. Again, we don't have to be very bright to see that:
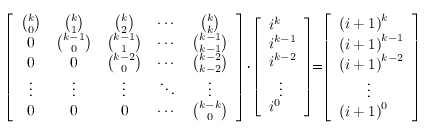
That looks nice. But let's get our ai sequence into play:
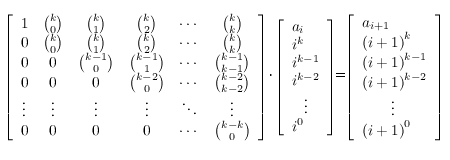
Now, because matrix multiplication is associative, we can compute the n-th power of our magic matrix in time O(k3 * log n) and then multiply it by the vector for a1 (it will contain only ones) to get an. Well, that definitely didn't hurt us. There were of course many different approaches. We could for example use Lagrange's polynomial interpolation (as the given sum is of course a polynomial) or use a different recursion then the one described here (please see the klopyrev's solution for a reference). There was also a solution based on Bernoulli numbers - use Google to find it! HouseProtection


Used as: Division One - Level Three:
Value 1000 Submission Rate 92 / 560 (16.43%) Success Rate 51 / 92 (55.43%) High Score ACRush for 830.85 points (13 mins 23 secs) Average Score 628.48 (for 51 correct submissions)
Let's think for a moment about an easier version of the problem - let's think how we can find the biggest
number of radars we're able to place for some given range. To begin, we'll place radars in all possible
points. Now, we want to remove the smallest number of radars in such way, that in the remaining set there
won't be any pair of intersecting radars that have different colors. That starts to sound like a vertex cover
problem - let's build a graph out of our radars and let's connect two radars of different colors with an edge if
their areas intersect. The general vertex cover problem is a well-known NP-complete problem. But, luckily, we have
a bipartite graph here, so according to
Konig's theorem we know that the minimal vertex cover is equivalent to maximal matching. We know how to find
the latter, so let's return to the original problem.
The safety factor is defined by two values -the number of
radars and their range. So, let's try every possible number of radars and for each such number, let's find the
biggest range that allows us to place the radars. It isn't a surprise that we can do it with a binary search -
if we can place the radars setting them on radius r, we could also set them to any range smaller than
r. That was quick, but enough to pass - you can see the fastest, but very clear
implementation
of the above by ACRush.
However, we can get rid of
the binary search here. The observation is that in the optimal solution the range of the radars will be either
the given R or half of the distance between some two red and blue points. Why? If it was not the case,
we could increase the range to let the areas of some radars touch. Now, if we consider the possible ranges
in an increasing order, we don't have to cancel the matching every time we have a new range (provided, we use
an augmenting path algorithm) as we aren't removing any edges from the graph, but just adding the new ones, so
the matching we have so far is ok with a new graph. For
every range candidate, we will compute the biggest number of radars we can place. That's enough to compute
the answer. This solution has time complexity of O(n4) instead of O(n4 * binary search). You
can see a nice implementation
of this by pparys.
