Match summary

This match was harder than usual. All three problems in the first division proved to be rather tricky. Only 229 coders solved the so-called easy problem, 40 solved the medium, while only 10 coders successfully restored expression in the hard one.

Petr and elizarov were the only two coders who solved all three problems. Petr won the match with a wide margin, thanks to his fast 1000-pointer. They were followed by andrewzta. His fourth place showing allowed kalinov to reach the target rating -- congratulations! And an amazing +500 at the challenge phase lifted gevak up to the fifth place.

In the second division Astein enjoyed the victory with the fastest hard and +200 in challenges.

The Problems

IrreducibleNumber

Used as: Division Two - Level One:

Value 250

Submission Rate 426 / 496 (85.89%)

Success Rate 277 / 426 (65.02%)

High Score hungson175 for 247.92 points (2 mins 36 secs)

Average Score 197.92 (for 277 correct submissions)

Actually, this problem can be solved efficiently with the size of A much greater than 3. The solution is as follows:

Sort(A);
N = 0; K = 0;
while K < A.size and A[K] ≤ N+1 do
    N = N + A[K]
    K = K+1
return N+1

To prove this solution, let's prove the following property: on each step of the algorithm above, only non-negative integers less or equal to N can be represented as a required sum of first K elements from A.

When N = K = 0, it's obvious. Moreover, if on some step A[K] appears to be greater than N+1, it implies that the number N+1 is irreducible. Indeed, N+1 cannot be represented as a sum of first K elements from A, and all other elements from A are greater than N+1, so N+1 is irreducible.

In the other case, if A[K] ≤ N+1, all the integers in range from N+1 to N+A[k] can also be represented as a sum of first K+1 elements. The desired representation can be obtained by adding A[K] to the representation of the respected element in range from 1 to N.

RoadsAndFools

Used as: Division Two - Level Two:

Value 500

Submission Rate 200 / 496 (40.32%)

Success Rate 64 / 200 (32.00%)

High Score Melbob for 366.59 points (18 mins 37 secs)

Average Score 249.90 (for 64 correct submissions)

Used as: Division One - Level One:

Value 250

Submission Rate 403 / 452 (89.16%)

Success Rate 229 / 403 (56.82%)

High Score Spieler for 242.15 points (5 mins 8 secs)

Average Score 162.61 (for 229 correct submissions)

This problems reformulates as follows: given a sequence A[1..N] and integer length, your task is to construct a new sequence B[1..N], where for each index i either B[i] = A[i] or B[i] = length - A[i] and sequence B is strictly increasing.

Note that if such a sequence exists, then the lexicographically first of them will have the following structure: B[i] = min( A[i], length - A[i]) for each index i from 1 to some integer K ≤ N and B[i] = max( A[i], length - A[i]) for each i > K. So let's try to take B[i] = min( A[i], length - A[i]) while it's possible and then switch to max( A[i], length - A[i]).

The following pseudocode illustrates this approach:

B[1] = min( A[1], length - A[1]) 
for i = 2 to N do begin 
    minimum = min( A[i], length - A[i]) 
    maximum = max( A[i], length - A[i]) 
    if minimum>B[i-1] then B[i] = minimum 
    else if maximum>B[i-1] then B[i] = maximum 
    else return "NO SOLUTION"                 
end

How do you check if the solution is unique? It's simple: for each index i try to replace B[i] with length - B[i] and see if the result remains strictly increasing. The only corner case is when B[i] = length/2, such indices i mustn't be checked. It is sufficient, because if B is strictly increasing and you replace more than two of its element with its difference with length, the resulting sequence won't be able to be strictly increasing.

UnrepeatableWords

Used as: Division Two - Level Three:

Value 1000

Submission Rate 15 / 496 (3.02%)

Success Rate 7 / 15 (46.67%)

High Score Astein for 878.91 points (10 mins 51 secs)

Average Score 610.85 (for 7 correct submissions)

The solution of this problem is based on the backtracking. Suppose that we have already found k-unrepeatable word of length n-1 and we want to extend it to length n. Let's try to add character 'A' and check, whether the resulting word will be k-unrepeateble or not. If not, we'll try letter 'B' and so on. If we can't extend our word to length n by adding any allowed character, we'll have to move one step back, to the word of length n-2.

The general scheme of the solution looks like this:

for i = 0 to N-1 do Res[i] = '?'; 
pos = 0; 
while true begin 
    if pos<0 then 
        no solution; 
    if pos=N then 
        solution found; 
    if Res[pos]=='?' then 
         Res[pos] = 'A'; 
        if checkUnrepeatable(pos) then 
             pos = pos + 1; 
    else if Res[pos]<'A' + allowed then 
         Res[pos] = next_character(Res[pos]); 
        if checkUnrepeatable(pos) then 
             pos = pos + 1; 
    else 
         Res[pos] = '?'; 
         pos = pos - 1; 
end while;

Now we need to implement the checkUnrepeatable function.

Note, that in our algorithm if checkUnrepeatable(pos), where pos > 0, is called, then checkUnrepeatable(pos-1) is true. So, we only need to try all the subwords with length 1, 2, .., (pos+1) / k that end at position pos. For clarity, see the picture below:

Here, for k=3 and pos=8 possible length of the subword could be 3, 2 or 1.

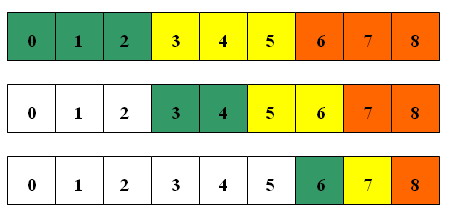
For every possible length we need to check whether all k subwords are the same. A good optimization is to compare all the first characters of these words, then all the second characters and so on. The comparison of k characters can be done at O(k). So the whole checkUnrepeatable will take at most O(pos^2).

It took Astein less then 11 minutes to accomplish this approach. See his solution for clear implementation.

Survived

Used as: Division One - Level Two:

Value 500

Submission Rate 215 / 452 (47.57%)

Success Rate 40 / 215 (18.60%)

High Score wd.h for 433.46 points (11 mins 29 secs)

Average Score 306.92 (for 40 correct submissions)

Let V be our own velocity and U be the velocity of the ocean stream, and we are supposed to reach point (x, y).

First of all, let's consider all corner cases. If x = y = 0 return 0, else if V = 0 then we still may achieve point (x, y) if x > 0, y=0 and U > 0.

Due to the laws of relative motion, we may consider our own velocity and stream's velocity separately. Let's suppose that the minimal time necessary to reach the desired destination is T. During this time the stream will move us to point (UT, 0). So, the task reduces to reachability of point (x, y) from point (UT, 0) in time T with speed V. In other words, we need to solve the equation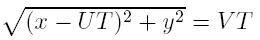

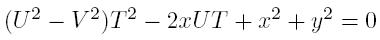
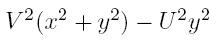
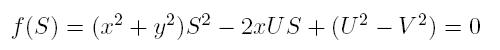
and find its minimal non-negative root. We can simply obtain the following equation:

We should consider two general cases. If U = V then this equation is linear and has only one root. In the other case, the equation is quadratic and its discriminant equals:

We need to check if the discriminant is less than zero (in this case there is no solution), equals to zero (one root) or is greater than zero (two roots). We may choose only positive roots and if no such roots exist there is no solution. If more than one positive root exists we need to choose the smaller one. See wd.h's solution for the details.

Another approach is based on the Viete's formulas. By making a substitution S=1/T we can obtain quadric equation with positive leading coefficient:

Let's denote coefficients of this equation as A, B and C. If discriminant B*B-4*A*C is less than zero, no solution exists. In the other case, let s1 and s2 be the (possible equal) roots of the equation f(S)=0. According to Viete's formulas, s1*s2 = C/A and s1+s2 = -B/A. Note, that if s1*s2 < 0 exactly one positive root exists. In the other case, if both s1 and s2 have the same sign, we need their sum to be greater than zero. Since A>0, we only need to demand that or C < 0, or C ≥ 0 and B < 0. See dyatlov's solution for the details.

RestoreExpression

Used as: Division One - Level Three:

Value 1000

Submission Rate 48 / 452 (10.62%)

Success Rate 10 / 48 (20.83%)

High Score Petr for 866.99 points (11 mins 29 secs)

Average Score 605.78 (for 10 correct submissions)

Attention and accuracy are the keys to solve this problem. First of all, let's parse our "A+B=C" expression and pick out three masks: A, B and C. Let's add leading zeroes to make their lengths equal, and denote this length as Len. To make the implementation easier, let's introduce the can(string X, int Pos, char D) that checks, if it is possible to apply digit D at position Pos to mask X. This function must also prevent the appearing of leading zeroes. Now we are going to write recursive solvePosition(int Pos, int ToAdd) function, where Pos is the current position in masks and ToAdd equls to 0 or 1. It checks, if it's possible to restore the expression "A[Pos..N-1]+B[Pos..N-1]=DC[Pos..N-1]".
The rough plan of this function looks like this.

bool solvePosition(int Pos, int ToAdd){
    if(Pos==Len && ToAdd==0){
        we've found a solution!
        let's check if it's better than those we've already found
        return true;
    }
    if(Pos==Len && ToAdd==0)
        return false;
    // pay attention to the order of the loops!
    for(int ci = 9; ci>=0; ci--)if(can(C, Pos, ci))
        for(int ai = 9; ai>=0; ai--)if(can(A, Pos, ai))
            for(int bi = 9; bi>=0; bi--)if(can(B, Pos, bi)){
                if(ai+bi == ToAdd*10+ci && solvePosition(Pos+1, 0)){
                    we can take
                    c[Pos] = (ai+bi)%10;
                    a[Pos] = ai;
                    b[Pos] = bi;
                }
                else if(ai+bi+1 == ToAdd*10+ci && solvePosition(Pos+1, 1)){
                    we can take
                    c[Pos] = (ai+bi)%10;
                    a[Pos] = ai;
                    b[Pos] = bi;
                }
        }
}

Now all we need is just to call solvePosition(0,0). This solution will work, but too slowly. Fortunately, the following two tricks will make it work almost instant. First, note that if we've already found the solution for current ci and ai we do not need to check the others, because they are less than ours. (But we still need to finish the iteration of the bi-loop!)
The second trick involves the memoization. Note, that the result of solvePositon call do not depend on current values of ai, bi and ci. So if it returns false, we'll be able to store this result, and we won't call it again. (But we still need to make the "true-calls," even if we already know that it will return true!) Now, it's easy to see that the whole soution will make at most 2^Len calls of solvePosition, which is acceptable.

See kalinov's solution for a clear implementation.

By Pawa
TopCoder Member